
【题目】已知:抛物线C1:y=ax2+bx+c经过点A(-1,0)、B(3,0)、C(0,-3).
(1)求抛物线C1的解析式;
(2)将抛物线C1向左平移几个单位长度,可使所得的抛物线C2经过坐标原点,并求出C2的解析式;
(3)把抛物线C1绕点A(-1,O)旋转180°,写出所得抛物线C3顶点D的坐标.
【答案】(1)抛物线C1:![]() (2)向左平移3个单位长度抛物线C2:
(2)向左平移3个单位长度抛物线C2:![]() ;(3)(-3,4).
;(3)(-3,4).
【解析】
(1)根据y=ax2+bx+c经过点A(-1,0)、B(3,0)、C(0,-3)列出三元一次方程,解得a、b、c;
(2)求出原函数的图象对称轴,然后运用平移知识解答;
(3)根据旋转的知识点,求出D点坐标.
(1)∵y=ax2+bx+c经过点A(-1,0)、B(3,0)、C(0,-3).
∴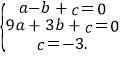
解得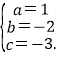
∴所求抛物线C1的解析式为:y=x2-2x-3;
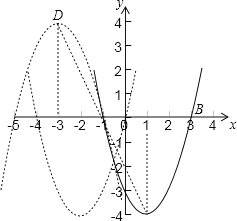
(2)抛物线C1向左平移3个单位长度,可使得到的抛物线C2经过坐标原点
所求抛物线C2的解析式为:y=x(x+4)=x2+4x;
(3)D点的坐标为(-3,4).


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
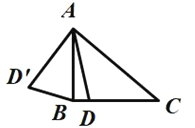
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 上的动点,将线段
上的动点,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 至
至![]() ,连接
,连接![]() .已知
.已知![]() ,设
,设![]() 为
为![]() ,
,![]() 为
为![]() .
.
小明根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究,下面是小明的探究过程.请补充完整(说明:解答中所填数值均保留一位小数)
的变化而变化的规律进行了探究,下面是小明的探究过程.请补充完整(说明:解答中所填数值均保留一位小数)
(1)通过取点、画图、测量,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
| 0 | 0.5 | 0.7 | 1.0 | 1.5 | 2.0 | 2.3 |
| 1.7 | 1.3 | 1.1 |
| 0.7 | 0.9 | 1.1 |
![]() 的值约为____________;
的值约为____________;
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图像.

(3)结合画出的函数图像,解决问题:
①线段![]() 的长度的最小值约为____________
的长度的最小值约为____________![]() ;
;
②![]() ,则
,则![]() 的长度
的长度![]() 的取值范围是____________.
的取值范围是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在下列横线上:
每件销售利润____________________________;
销售量y(件)____________________________;
销售玩具获得利润w(元)____________________________;
(2)销售单价定为多少时,利润最大?
(3)若商场获得了10000元销售利润,求该玩具销售单价x应定为多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B![]() 90°,AB
90°,AB![]() 4,BC
4,BC![]() 2,以AC为边作△ACE,∠ACE
2,以AC为边作△ACE,∠ACE![]() 90°,AC=CE,延长BC至点D,使CD
90°,AC=CE,延长BC至点D,使CD![]() 5,连接DE.求证:△ABC∽△CED.
5,连接DE.求证:△ABC∽△CED.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某茶叶销售商计划将m罐茶叶按甲、乙两种礼品盒包装出售,其中甲种礼品盒每盒装4罐,每盒售价240元;乙种礼品盒每盒装6罐,每盒售价300元,恰好全部装完.已知每罐茶叶的成本价为30元,设甲种礼品盒的数量为x盒,乙种礼品盒的数量为y盒.
(1)当m=120时.
①求y关于x的函数关系式.
②若120罐茶叶全部售出后的总利润不低于3000元,则甲种礼品盒的数量至少要多少盒?
(2)若m罐茶叶全部售出后平均每罐的利润恰好为24元,且甲、乙两种礼品盒的数量和不超过69盒,求m的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com