
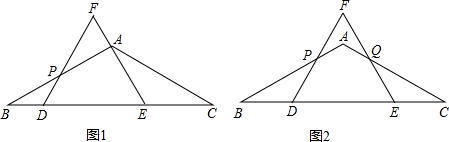
分析 (1)过点A作AG⊥BC于G,由锐角三角函数求得AB=2$\sqrt{3}$,BG=$\frac{1}{2}$BC=3,再根据三角函数列方程求解.
(2)根据点P的不同位置分类讨论,由三角形的面积公式列方程求解;
(3)当EF过A点时,PA⊥AC,由(1)解得:t=1,当点E,C重合时,即点P到DF的距离=AP=$\sqrt{3}$t-2$\sqrt{3}$,由直角三角形的性质列方程2($\sqrt{3}t-2\sqrt{3}$)=4$\sqrt{3}$-$\sqrt{3}$t,求得t=$\frac{8}{3}$,当P到BC的距离=PA,列方程$\frac{\sqrt{3}t}{2}$=2$\sqrt{3}$-$\sqrt{3}t$,求得t=$\frac{4}{3}$,当点P到EF的距离=PA时,列方程$\frac{\sqrt{3}(t-1)}{2}$=$\sqrt{3}$t-2$\sqrt{3}$,求得t=3.
解答 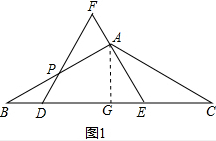 解:(1)过点A作AG⊥BC于G,
解:(1)过点A作AG⊥BC于G,
∵∠B=30°,
∴AB=2$\sqrt{3}$,
∴BG=$\frac{1}{2}$BC=3,
∵△DEF为正三角形,
∴∠F=∠FDE=60°,
∵∠B=30°,
∴∠BPD=∠FPA=30°
∴∠FAP=∠BAE=90°,
由题意得:PB=$\sqrt{3}$t,AP=2$\sqrt{3}$-$\sqrt{3}$t,
∴AE=2,
∴AF=1,
∴tan∠FPA=$\frac{AF}{AP}$=$\frac{1}{2\sqrt{3}-\sqrt{3}t}$=$\frac{\sqrt{3}}{3}$,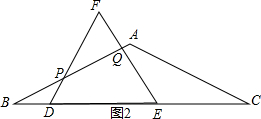
∴t=1;
(2)当0≤t≤1时,如图2,
由(1)得:EF⊥AB,AB=2$\sqrt{3}$,
∵PB=$\sqrt{3}$t,∴PD=t,FP=3-t,FQ=$\frac{3-t}{2}$,PQ=$\frac{\sqrt{3}}{2}$(3-t),
∴S=S△DEF-S△PQF=$\frac{1}{2}$×$3×\frac{3\sqrt{3}}{2}$-$\frac{1}{2}$•$\frac{3-t}{2}$$•\frac{\sqrt{3}}{2}$(3-t),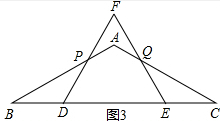
∴S=-$\frac{\sqrt{3}}{8}$t2$+\frac{3\sqrt{3}}{4}t+\frac{9\sqrt{3}}{8}$;
当1<t≤2时,如图3,
∵BP=$\sqrt{3}$t,
∴BD=t,
∴CE=6-3-t=3-t,
∴CQ=3$\sqrt{3}$-$\sqrt{3}$t,
∴S=S△ABC-S△BPD-S△ECH=$\frac{1}{2}×6×\sqrt{3}$-$\frac{1}{2}$$•\sqrt{3}t•\frac{1}{2}t$-$\frac{1}{2}(3\sqrt{3}-\sqrt{3}t)•\frac{3-t}{2}$,
∴S=-$\frac{\sqrt{3}}{2}$t2$+\frac{3\sqrt{3}}{2}$t$+\frac{3\sqrt{3}}{4}$,
当2<t≤3时,如图4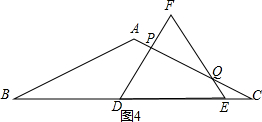 ,
,
由(1)得:DF⊥AC,
∵AP=$\sqrt{3}t-2\sqrt{3}$,
∴PC=2$\sqrt{3}-(\sqrt{3}t-2\sqrt{3})$=4$\sqrt{3}-\sqrt{3}t$,
∴PD=4-t,
∴PF=t-1,
∴PQ=$\sqrt{3}(t-1)$,
∴S=S△DEF-S△PFQ=$\frac{1}{2}×3×\frac{3\sqrt{3}}{2}$-$\frac{1}{2}•(t-1)•\sqrt{3}(t-1)$,
∴S=-$\frac{\sqrt{3}}{2}$t2$+\sqrt{3}t+\frac{7\sqrt{3}}{4}$;
综上所述:S=-$\frac{\sqrt{3}}{8}$t2$+\frac{3\sqrt{3}}{4}t+\frac{9\sqrt{3}}{8}$(0≤t≤1),
S=-$\frac{\sqrt{3}}{2}$t2$+\frac{3\sqrt{3}}{2}$t$+\frac{3\sqrt{3}}{4}$(1<t≤2),
S=-$\frac{\sqrt{3}}{2}$t2$+\sqrt{3}t+\frac{7\sqrt{3}}{4}$(2<t≤3);
(3)当EF过A点时,PA⊥AC,
由(1)解得:t=1,
当点E,C重合时,
即点P到DF的距离=AP=$\sqrt{3}$t-2$\sqrt{3}$,
∵PC=4$\sqrt{3}$-$\sqrt{3}$t,
∴2AP=CP,
即:2($\sqrt{3}t-2\sqrt{3}$)=4$\sqrt{3}-\sqrt{3}t$,
解得:t=$\frac{8}{3}$,
当P到BC的距离=PA,
即;$\frac{\sqrt{3}t}{2}$=2$\sqrt{3}$-$\sqrt{3}t$,
解得:t=$\frac{4}{3}$,
当点P到EF的距离=PA时,
即:$\frac{\sqrt{3}(t-1)}{2}$=$\sqrt{3}$t-2$\sqrt{3}$,
解得:t=3,
∵2.5秒时运动结束,
∴当t=1,$\frac{4}{3}$时,使得以点P为圆心,AP为半径的圆与△FDE三边所在的直线相切.
点评 本题考查了等腰三角形的性质和等边三角形的性质,动点问题,三角函数,列方程等知识点,特别是(2)(3)两问要根据点P的本题位置求解.


科目:初中数学 来源: 题型:填空题
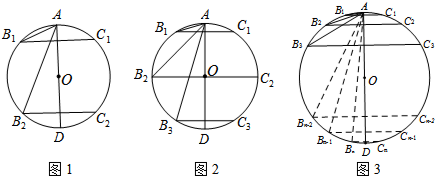
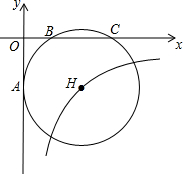 如图所示,经过B(2,0)、C(6,0)两点的⊙H与y轴的负半轴相切于点A,双曲线y=$\frac{k}{x}$经过圆心H,则k=-8$\sqrt{3}$.
如图所示,经过B(2,0)、C(6,0)两点的⊙H与y轴的负半轴相切于点A,双曲线y=$\frac{k}{x}$经过圆心H,则k=-8$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
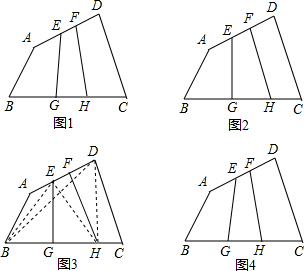 【提出问题】如图①,在四边形ABCD中,点E、F是AD的n等分点中最中间2个,点G、H是BC的n等分点中最中间2个,(其中n为奇数),连接EG、FH,那么S四边形EFHG与S四边形ABCD之间有什么关系呢?
【提出问题】如图①,在四边形ABCD中,点E、F是AD的n等分点中最中间2个,点G、H是BC的n等分点中最中间2个,(其中n为奇数),连接EG、FH,那么S四边形EFHG与S四边形ABCD之间有什么关系呢?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 握手图标 | 握手人数 | 握手次数 |
 | 2 | 1 |
 | 3 | 3=1+2 |
 | 4 | 6=1+2+3 |
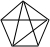 | 5 | 10=1+2+3+4 |
| … | … | … |
| … | N | P=1+2+3+…+(n+1) |
| 图标 | 直线条数 | 交点个数 |
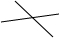 | 2 | 1 |
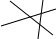 | 3 | 3=1+2 |
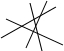 | 4 | |
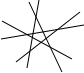 | 5 | |
| … | … | … |
| … | n |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
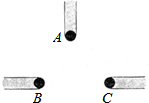 (1)如图是小刚(A)、小明(B)、小勇(C)和他们各自影子的俯视图,他们所构成三角形地形的内部有一盏路灯,你认为如图是在白天阳光下的俯视图还是在晚上这盏路灯下的俯视图?
(1)如图是小刚(A)、小明(B)、小勇(C)和他们各自影子的俯视图,他们所构成三角形地形的内部有一盏路灯,你认为如图是在白天阳光下的俯视图还是在晚上这盏路灯下的俯视图?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com