
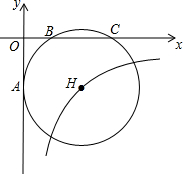
 如图所示,经过B(2,0)、C(6,0)两点的⊙H与y轴的负半轴相切于点A,双曲线y=$\frac{k}{x}$经过圆心H,则k=-8$\sqrt{3}$.
如图所示,经过B(2,0)、C(6,0)两点的⊙H与y轴的负半轴相切于点A,双曲线y=$\frac{k}{x}$经过圆心H,则k=-8$\sqrt{3}$. 分析 过H作HE⊥BC于点E,可求得E点坐标和圆的半径,连接BH,在Rt△BEH中,可求得HE的长,可求得H点坐标,代入双曲线解析式可求得k.
解答 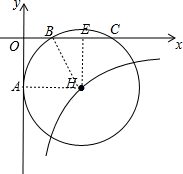 解:
解:
过H作HE⊥BC于点E,连接BH,AH,如图,
∵B(2,0),C(6,0),
∴BC=4,
∴BE=$\frac{1}{2}$BC=2,
∴OE=OB+BE=2+2=4,
又⊙H与y轴切于点A,
∴AH⊥y轴,
∴AH=OE=4,
∴BH=4,
在Rt△BEH中,BE=2,BH=4,
∴HE=2$\sqrt{3}$,
∴H点坐标为(4,-2$\sqrt{3}$),
∵y=$\frac{k}{x}$经过圆心H,
∴k=-8$\sqrt{3}$,
故答案为:-8$\sqrt{3}$.
点评 本题主要考查切线的性质和垂径定理,由条件求得圆的半径从而求得H点的坐标是解题的关键.


 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:填空题
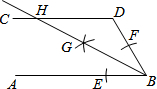 如图,AB∥CD,以点B为圆心,小于DB长为半径作圆弧,分别交BA、BD于点E、F,再分别以点E、F为圆心,大于$\frac{1}{2}$EF长为半径作圆弧,两弧交于点G,作射线BG交CD于点H.若∠D=116°,则∠DHB的大小为32度.
如图,AB∥CD,以点B为圆心,小于DB长为半径作圆弧,分别交BA、BD于点E、F,再分别以点E、F为圆心,大于$\frac{1}{2}$EF长为半径作圆弧,两弧交于点G,作射线BG交CD于点H.若∠D=116°,则∠DHB的大小为32度.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 16$\sqrt{3}$m2 | B. | 32$\sqrt{3}$m2 | C. | $\sqrt{3}$m2 | D. | 96$\sqrt{3}$m2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
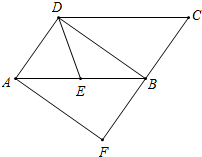 如图,在?ABCD中,E为边AB的中点,BD是对角线,AF∥DB交CB的延长线于F.若DE=BE,则四边形AFBD是什么特殊四边形?并证明你的结论.
如图,在?ABCD中,E为边AB的中点,BD是对角线,AF∥DB交CB的延长线于F.若DE=BE,则四边形AFBD是什么特殊四边形?并证明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
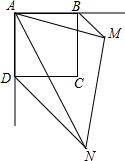 已知:如图,正方形ABCD,BM、DN分别是正方形的两个外角平分线,∠MAN=45°,将∠MAN绕着正方形的顶点A旋转,边AM、AN分别交两条角平分线于点M、N,联结MN.
已知:如图,正方形ABCD,BM、DN分别是正方形的两个外角平分线,∠MAN=45°,将∠MAN绕着正方形的顶点A旋转,边AM、AN分别交两条角平分线于点M、N,联结MN.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
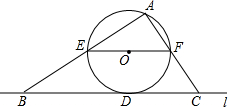 如图,直线L与⊙O相切于点D.过圆心O作EF∥L交⊙O于E、F两点,点A是⊙O上一点,连接AE、AF.并分别延长交直线L于 B、C两点.
如图,直线L与⊙O相切于点D.过圆心O作EF∥L交⊙O于E、F两点,点A是⊙O上一点,连接AE、AF.并分别延长交直线L于 B、C两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com