Question

17．用形状、大小完全相同的一种或几种平面图形进行拼接，使图形之间没有空隙，也没有重叠地铺成一片，我们称之为图形的密铺．如图，是用全等的三角形或四边形材料密铺而成的地面．

思考：
（1）用全等的正五边形材料能够密铺地面吗？
（2）用边长相同的m个正三角形和n个正方形材料组合密铺地面应满足的方程是3m+2n=12，此时m、n的值存在吗？若存在，请画出密铺地面的示意图．
（3）在边长相同的正三角形、正方形、正六边形材料中，哪几种材料组合能够密铺地面？

Answer 1

分析 正多边形的组合能否铺满地面，关键是看位于同一顶点处的几个角之和能否为360°．若能，则说明能铺满；反之，则说明不能铺满．

解答 解：（1）∵正五边形的一个内角度数为180-360÷5=108°，不是360°的约数，∴不能密铺地面；
（2）∵∵正三角形的内角为60°，正方形的内角为90°，能组成360°，∴60°m+90°n=360，
∴满足的方程是2m+3n=12，
∵当m=3，n=2时，2m+3n=12，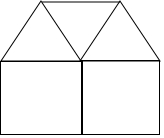
∴m、n的值存在，如图，
故答案为：2m+3n=12；

（3）∵正方形的每个内角是90°，正六边形的每个内角是120°，90m+120n=360°，m=4-$\frac{4}{3}$n，显然n取任何整数时，m不能得正整数，∴不能铺满，符合题意；
∵正三角形的每个内角是60°，正方形的每个内角是90°，∵3×60°+2×90°=360°，∴能铺满地面，
∵正三角形的每个内角是60°，正六边形的每个内角是120度，∵2×60°+2×120°=360°，∴能铺满地面，
正三角形的每个内角是60°，正方形的每个内角是90°，正六边形的每个内角是120度，∵60°+2×90°+120°=360°，∴能铺满地面．
∴正三角形与正方形，正三角形与正六边形，正三角形与正方形与正六边形组合能够密铺地面．

点评 本题考查平面镶嵌的知识．几何图形镶嵌成平面的关键是：围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角．