
【题目】从![]() 地向
地向![]() 地打长途电话,按时收费,3分钟内收费2.7元,3分钟后,每通话1分钟收费1.2元.某人在
地打长途电话,按时收费,3分钟内收费2.7元,3分钟后,每通话1分钟收费1.2元.某人在![]() 地向
地向![]() 地打电话共用了
地打电话共用了![]() ,且
,且![]() 为整数)分钟,话费为
为整数)分钟,话费为![]() 元.
元.
(1)写出![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(2)若通话5分钟,则需要话费多少元?
(3)若某次通话费用为8.7元,则他通话多少分钟?
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,添加一个条件,仍不能证明四边形BECF为正方形的是

A. BC=AC B. CF⊥BF C. BD=DF D. AC=BF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】结合数轴与绝对值的知识回答下列问题:
(1)表示﹣3和2两点之间的距离是_____;一般地,数轴上表示数m和数n的两点之间的距离等于|m﹣n|.
如果|a+2|=3,那么a=_____;
(2)若数轴上表示数a的点位于﹣4与2之间,则|a+4|+|a﹣2|的值为_____;
(3)利用数轴找出所有符合条件的整数点x,使得|x+2|+|x﹣5|=7,这些点表示的数的和是_____;
(4)当a=_____时,|a+3|+|a﹣1|+|a﹣4|的值最小,最小值是_____.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
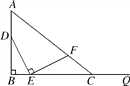
【题目】如图,AB=4,射线BQ和AB互相垂直,点D是AB上的一个动点,点E在射线BQ上,BE=![]() DB,作EF⊥DE,并截取EF=DE,连接AF并延长交射线BQ于点C.设BE=x,BC=y,则y关于x的函数解析式为______________.
DB,作EF⊥DE,并截取EF=DE,连接AF并延长交射线BQ于点C.设BE=x,BC=y,则y关于x的函数解析式为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知b是最小的正整数,且a、c满足|a+1|+(c+6)2=0.
(1)填空:a= ,b= ,c= ;
(2)a、b、c在数轴上所对应的点分别为A、B、C,P是数轴上点A、B之间一动点(不与点A、B重合),其对应的数为x,|x+1|+|x﹣1|= ;
(3)在(1)、(2)的条件下,点A、B、C开始在数轴上同时运动,若点C和点A分别以每秒6个单位长度和2个单位长度的速度向左运动,点B以每秒2个单位长度的速度向右运动,假设t秒钟过后,若点A与点C之间的距离表示为AC,点A与B之间的距离表示为AB.请问:AC﹣AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.

查看答案和解析>>
科目:初中数学 来源: 题型:
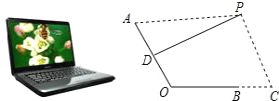
【题目】如图是一台放置在水平桌面上的笔记本电脑,将其侧面抽象成如右图所示的几何图形,若显示屏所在面的侧边AO与键盘所在面的侧边BO长均为24cm,点P为眼睛所在位置,D为AO的中点,连接PD,当PD?AO时,称点P为“最佳视角点”,作PC?BC,垂足C在OB的延长线上,且BC=12cm.
(1)当PA=45cm时,求PC的长;
(2)若?AOC=120°时,“最佳视角点”P在直线PC上的位置会发生什么变化?此时PC的长是多少?请通过计算说明.(结果精确到0.1cm,可用科学计算器,参考数据: ![]() ,
, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:﹣4,|﹣2|,﹣2,﹣(﹣3.5),0,![]() .
.
(1)在如图所示的数轴上表示出以上各数;
![]()
(2)比较以上各数的大小,用“<”号连接起来;
_____<_____<______<______<______<______
(3)在以上各数中选择恰当的数填在图中这两个圈的(重叠)部分.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD、正方形A1B1C1D1、正方形A2B2C2D2均位于第一象限内,它们的边平行于x轴或y轴,其中点A、A1、A2在直线OM上,点C、C1、C2在直线ON上,O为坐标原点,已知点A的坐标为(3,3),正方形ABCD的边长为1.若正方形A2B2C2D2的边长为2011,则点B2的坐标为___________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com