

分析 (1)由y与x的函数图象可以得到各段的函数解析式,从而可以求得第10天的销售量和销售总额;
(2)由y与x的函数图象可以设出各段的函数解析式,再根据图象中的数据可以得到y与x的函数关系式;
(3)由(2)中的函数解析式可以得到日销售量不低于24kg的时间段,由P与x的函数图象可以得到此期间最高单价是多少.
解答 解:(1)设0≤x≤15时,y与x之间的函数解析式为y=kx,
则15k=30,得k=2,
故0≤x≤15时,y与x之间的函数解析式为y=2x,
当x=10时,y=2×10=20千克,此时的销售单价p=10,故此时销售总额为:20×10=200元,
故答案为:20;200.
(2)设0≤x≤15时,y与x之间的函数解析式为y=kx,
则15k=30,得k=2,
故0≤x≤15时,y与x之间的函数解析式为y=2x,
设15≤x≤20时,y与x之间的函数解析式为y=mx+n,
则$\left\{\begin{array}{l}{15m+n=30}\\{20m+n=0}\end{array}\right.$
解得m=-6,n=120,
故15≤x≤20时,y与x之间的函数解析式为y=-6x+120,
由上可得,y与x之间的函数解析式为:y=$\left\{\begin{array}{l}{2x}&{(0≤x≤15)}\\{-6x+120}&{(15≤x≤20)}\end{array}\right.$.
(3)令2x≥24,得x≥12,则12≤x≤15,
令-6x+120≥24,得x≤16,则15≤x≤16,
∴12≤x≤16,
∴16-12+1=5(天)
由p于x的函数图象可知,当10≤x≤20时,p随x的增大而减小,
∴x=12时,销售单价最高,
设10≤x≤20时,p与x之间的函数解析式为:p=ax+b,
则$\left\{\begin{array}{l}{10a+b=10}\\{20a+b=8}\end{array}\right.$
解得,a=$-\frac{1}{5}$,b=12,
∴10≤x≤20时,p与x之间的函数解析式为:p=$-\frac{1}{5}x+12$,
当x=12时,p=$-\frac{1}{5}×12+12=9.6$,
即最佳销售期共有5天,此期间最高销售单价为9.6元/千克.
点评 本题考查一次函数的应用,解题的关键是明确题意,列出相应的函数解析式,利用数形结合的思想解答问题.


科目:初中数学 来源: 题型:解答题
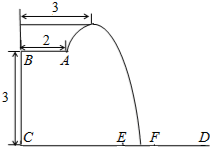 在2014年仁川亚运会上中国队包揽了跳水所有项目的金牌.过去十一届亚运会的跳水金牌也全部归于中国跳水队!优秀成绩的取得离不开艰辛的训练.某跳水运动员在进行一次跳水训练时,身体(看成一点)在空中的运动路线是如图所示的一条抛物线.已知跳板AB长为2米,跳板距水面CD高BC为3米,为安全和空中姿势优美,训练时跳水曲线在离起跳点水平距离1米时达到距水面最大高度4米,现以CD为横轴,CB为纵轴建立直角坐标系.
在2014年仁川亚运会上中国队包揽了跳水所有项目的金牌.过去十一届亚运会的跳水金牌也全部归于中国跳水队!优秀成绩的取得离不开艰辛的训练.某跳水运动员在进行一次跳水训练时,身体(看成一点)在空中的运动路线是如图所示的一条抛物线.已知跳板AB长为2米,跳板距水面CD高BC为3米,为安全和空中姿势优美,训练时跳水曲线在离起跳点水平距离1米时达到距水面最大高度4米,现以CD为横轴,CB为纵轴建立直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在四边形OABC中,CB∥OA,∠COA=90°,CB=3,OA=6,BA=3$\sqrt{5}$.分别以OA、OC边所在直线为x轴、y轴建立如图所示的平面直角坐标系.
在四边形OABC中,CB∥OA,∠COA=90°,CB=3,OA=6,BA=3$\sqrt{5}$.分别以OA、OC边所在直线为x轴、y轴建立如图所示的平面直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 0 | C. | -1 | D. | $\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com