
 在四边形OABC中,CB∥OA,∠COA=90°,CB=3,OA=6,BA=3$\sqrt{5}$.分别以OA、OC边所在直线为x轴、y轴建立如图所示的平面直角坐标系.
在四边形OABC中,CB∥OA,∠COA=90°,CB=3,OA=6,BA=3$\sqrt{5}$.分别以OA、OC边所在直线为x轴、y轴建立如图所示的平面直角坐标系.分析 (1)作BH⊥OA于H,根据矩形的性质求出OH的长,根据勾股定理求出BH的长,得到点B的坐标;
(2)作EG⊥OA于G,得到△OGE∽△OHB,根据题意和相似三角形的性质求出点E、D的坐标,运用待定系数法求出直线DE的解析式;
(3)作MP⊥y轴于点P,得到△MPD∽△FOD,根据相似三角形的性质和勾股定理计算即可.
解答 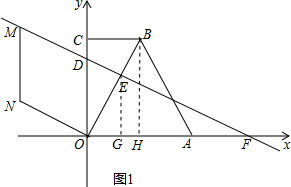 解:如图1,作BH⊥OA于H,则四边形OHBC为矩形,
解:如图1,作BH⊥OA于H,则四边形OHBC为矩形,
∴OH=CB=3,
∴AH=OA-OH=3,
∴BH=$\sqrt{B{A}^{2}-A{H}^{2}}$=6,
∴点B的坐标为(3,6);
(2)如图1,作EG⊥OA于G,则EG∥BH,
∴△OGE∽△OHB,
∴$\frac{OE}{OB}$=$\frac{OG}{OH}$=$\frac{EG}{BH}$,
∵OE=2EB,
∴$\frac{OE}{OB}$=$\frac{2}{3}$,又OH=3,BH=6,
∴OG=2,EG=4,
∴点E的坐标为(2,4),
∵OC=BH=6,OD=5,
∴点D的坐标为(0,5),
设直线DE的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{2k+b=4}\\{b=5}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=5}\end{array}\right.$,
∴直线DE的解析式为y=-$\frac{1}{2}$x+5;
(3)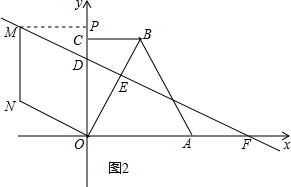 如图2,作MP⊥y轴于点P,
如图2,作MP⊥y轴于点P,
∵四边形ODMN是菱形,
∴DM=MN=NO=OD=5,
∵MP∥OA,
∴△MPD∽△FOD,
∴$\frac{MP}{OF}$=$\frac{MD}{DF}$=$\frac{PD}{OD}$,
当y=0,即-$\frac{1}{2}$x+5=0时,x=10,
∴点F的坐标为(0,10),
∴DF=$\sqrt{O{D}^{2}+O{F}^{2}}$=5$\sqrt{5}$,
∴$\frac{MP}{10}$=$\frac{PD}{5}$=$\frac{5}{5\sqrt{5}}$,
解得,MP=2$\sqrt{5}$,PD=$\sqrt{5}$,
∴OP=5+$\sqrt{5}$,
∴N的坐标为(-2$\sqrt{5}$,$\sqrt{5}$).
点评 本题考查的是一次函数知识的综合运用,掌握矩形的性质定理、菱形的性质定理、相似三角形的判定和性质定理以及待定系数法求函数解析式的步骤是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
 如图,在矩形ABCD中,AB=3,BC=4,点E在BC边上运动,连结AE,过点D作DF⊥AE,垂足为F,设AE=x,DF=y,则能反映y与x之间函数关系的大致图象是( )
如图,在矩形ABCD中,AB=3,BC=4,点E在BC边上运动,连结AE,过点D作DF⊥AE,垂足为F,设AE=x,DF=y,则能反映y与x之间函数关系的大致图象是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3x-1=4x+2 | B. | 3x+1=4x-2 | C. | $\frac{x-1}{3}$=$\frac{x+2}{4}$ | D. | $\frac{x+1}{3}$=$\frac{x-2}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用26m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设BC=x m.
在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用26m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设BC=x m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
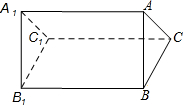 如图是一个三棱柱的图形,它共有五个面,其中三个面是长方形,两个面是三角形,请写出符合下列条件的棱(说明:每个空只需写出一条即可).
如图是一个三棱柱的图形,它共有五个面,其中三个面是长方形,两个面是三角形,请写出符合下列条件的棱(说明:每个空只需写出一条即可).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com