
 如图所示,在△ABC中,∠A=90°,∠ABC的平分线与∠ACB的平分线相交于点O,求∠BOC的度数.
如图所示,在△ABC中,∠A=90°,∠ABC的平分线与∠ACB的平分线相交于点O,求∠BOC的度数.  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,已知正方形OABC的边长为2,顶点A,C分别在x轴,y轴的正半轴上,E点是BC的中点,F是AB延长线上一点且FB=1.
如图,已知正方形OABC的边长为2,顶点A,C分别在x轴,y轴的正半轴上,E点是BC的中点,F是AB延长线上一点且FB=1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 周长相等的两个等边三角形全等 | B. | 斜边相等的两个直角三角形全等 | ||
| C. | 面积相等的两个三角形全等 | D. | 腰长相等的两个等腰三角形全等 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在△ABC中,∠A=30°,∠B=60°
已知:如图,在△ABC中,∠A=30°,∠B=60°查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AD是BC边上的中线.
如图,在△ABC中,AD是BC边上的中线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
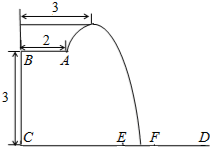 在2014年仁川亚运会上中国队包揽了跳水所有项目的金牌.过去十一届亚运会的跳水金牌也全部归于中国跳水队!优秀成绩的取得离不开艰辛的训练.某跳水运动员在进行一次跳水训练时,身体(看成一点)在空中的运动路线是如图所示的一条抛物线.已知跳板AB长为2米,跳板距水面CD高BC为3米,为安全和空中姿势优美,训练时跳水曲线在离起跳点水平距离1米时达到距水面最大高度4米,现以CD为横轴,CB为纵轴建立直角坐标系.
在2014年仁川亚运会上中国队包揽了跳水所有项目的金牌.过去十一届亚运会的跳水金牌也全部归于中国跳水队!优秀成绩的取得离不开艰辛的训练.某跳水运动员在进行一次跳水训练时,身体(看成一点)在空中的运动路线是如图所示的一条抛物线.已知跳板AB长为2米,跳板距水面CD高BC为3米,为安全和空中姿势优美,训练时跳水曲线在离起跳点水平距离1米时达到距水面最大高度4米,现以CD为横轴,CB为纵轴建立直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在四边形OABC中,CB∥OA,∠COA=90°,CB=3,OA=6,BA=3$\sqrt{5}$.分别以OA、OC边所在直线为x轴、y轴建立如图所示的平面直角坐标系.
在四边形OABC中,CB∥OA,∠COA=90°,CB=3,OA=6,BA=3$\sqrt{5}$.分别以OA、OC边所在直线为x轴、y轴建立如图所示的平面直角坐标系.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com