Question

8．如图，在△ABC中，AD是BC边上的中线．
①画出与△ACD关于D点成中心对称的三角形；
②找出与AC相等的线段；
③若AB=5，AC=3，AD=2，求线段BC的长．

Answer 1

分析 ①利用关于点D成中心对称的性质得出E点位置进而得出答案；
②利用对称的性质得出AC=BE；
③首先得出△ABE是直角三角形，进而利用勾股定理得出答案．

解答 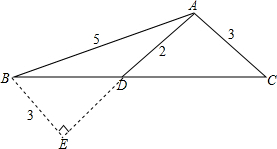解：①如图所致：
延长AD至E，使DE=AD，连接BE，则△EBD即为所求三角形；

②BE=AC；

③如图所示，由题意可得：AD=DE=2，
则AE=4，
故AB²=BE²+AE²，
则△ABE是直角三角形，
故BD=$\sqrt{B{E}^{2}+D{E}^{2}}$=$\sqrt{13}$，
∴BC=2BD=2$\sqrt{13}$．

点评 此题主要考查了旋转变换以及勾股定理的逆定理，正确利用关于点对称的性质得出对应点位置是解题关键．