
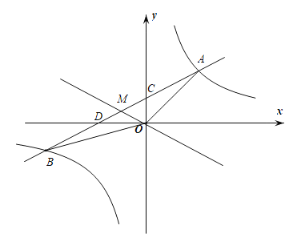
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 相交于
相交于![]() 、
、![]() 两点,与
两点,与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,已知
两点,已知![]() ,
,![]() 的面积为
的面积为![]() .
.
(1)求一次函数和反比例函数的解析式;
(2)连接![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 的中点,直线
的中点,直线![]() 向上平移
向上平移![]() 个单位将
个单位将![]() 的面积分成
的面积分成![]() 两部分,求
两部分,求![]() 的值.
的值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据一函数解析式求得OC的长,在Rt△OCD中,利用三角函数与勾股定理求得OD的长,即D点坐标,然后代入一次函数解析式求得k的值,即可得到一次函数解析式,再根据△BOD的面积求得B点纵坐标,代入一次函数得到B点坐标,然后代入反比例函数即可得解;
(2)先联立方程求得M点坐标,再设向上平移![]() 个单位得到的直线l′为:y=﹣
个单位得到的直线l′为:y=﹣![]() x+h,并设l′与线段AB交于点E,与线段OA交于点F.由题意可知:S△AEF:S△AOB=1:8,即S△AEF:S△AOM=1:4,得到E为AM中点,再将E点坐标代入y=﹣
x+h,并设l′与线段AB交于点E,与线段OA交于点F.由题意可知:S△AEF:S△AOB=1:8,即S△AEF:S△AOM=1:4,得到E为AM中点,再将E点坐标代入y=﹣![]() x+h求得h的值即可.
x+h求得h的值即可.
解:(1)令x=0,则y=1,
∴直线与y轴的交点C(0,1),
∴OC=1,
在Rt△OCD中,
∵![]() ,
,
∴CD=![]() =
=![]() ,
,
∴OD=![]() =2,
=2,
∴D(﹣2,0),
把D(﹣2,0)代入函数![]() ,解得:k=
,解得:k=![]() ,
,
∴一次函数的解析式为:![]() ,
,
又∵S△BOD=![]() ·OD·∣yB∣=1,
·OD·∣yB∣=1,
∴yB=﹣1,
把yB=﹣1代入一次函数得:xB=﹣4,
∴B(﹣4,﹣1),
把B(﹣4,﹣1)代入函数![]() ,解得:m=4,
,解得:m=4,
∴反比例函数的解析式为:![]() ;
;
(2)联立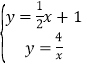 ,
,
解得:![]() 或
或![]() ,
,
∴A(2,2),B(﹣4,﹣1),
∴M(﹣1,![]() ),
),
∴直线OM的解析式为:y=﹣![]() x,
x,
设向上平移![]() 个单位得到的直线l′为:y=﹣
个单位得到的直线l′为:y=﹣![]() x+h,并设l′与线段AB交于点E,与线段OA交于点F.由题意可知:S△AEF:S△AOB=1:8,
x+h,并设l′与线段AB交于点E,与线段OA交于点F.由题意可知:S△AEF:S△AOB=1:8,
∴S△AEF:S△AOM=1:4,
又∵l′与OM平行,
∴E是线段AM的中点,
∴E(![]() ,
,![]() ),
),
把E(![]() ,
,![]() )代入y=﹣
)代入y=﹣![]() x+h得:
x+h得:![]() =﹣
=﹣![]() ×
×![]() +h,
+h,
∴h=![]() .
.


科目:初中数学 来源: 题型:
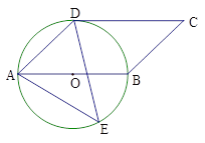
【题目】如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上任意一点,且CD切⊙O于点D.
(1)试求∠AED的度数.
(2)若⊙O的半径为![]() cm,试求△ADE面积的最大值.
cm,试求△ADE面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中的点P和图形G,给出如下的定义:若在图形G上存在一点Q ,使得P、Q之间的距离等于1,则称P为图形G的关联点.
中的点P和图形G,给出如下的定义:若在图形G上存在一点Q ,使得P、Q之间的距离等于1,则称P为图形G的关联点.
(1)当⊙O的半径为1时:
①点![]() ,
, ![]() ,
, ![]() 中,⊙O的关联点有_____________________.
中,⊙O的关联点有_____________________.
②直线经过(0,1)点,且与![]() 轴垂直,点P在直线上.若P是⊙O的关联点,求点P的横坐标
轴垂直,点P在直线上.若P是⊙O的关联点,求点P的横坐标![]() 的取值范围.
的取值范围.
(2)已知正方形ABCD的边长为4,中心为原点,正方形各边都与坐标轴垂直.若正方形各边上的点都是某个圆的关联点,求圆的半径![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市规定了每月用水量不超过18立方米和超过18立方米两种不同的收费标准,该市的用户每月应交水费![]() (元)是用水量
(元)是用水量![]() (立方米)的一次函数,其图象如图所示:
(立方米)的一次函数,其图象如图所示:
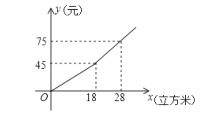
(1)若某月用水量超过18立方米,则每立方米的水费为__________元;
(2)当![]() 时,
时,![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)若小敏家三月份交水费81元,求这个月小敏家的用水量.
查看答案和解析>>
科目:初中数学 来源: 题型:
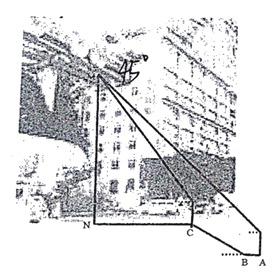
【题目】重庆李子坝轻轨站穿楼而过成网红,小明想要测量轻轨站穿楼时轨道与大楼连接处![]() 距离地面
距离地面![]() 的高度,他站在点
的高度,他站在点![]() 处测得轨道与大楼连接处顶端
处测得轨道与大楼连接处顶端![]() 的仰角为
的仰角为![]() ,向前走了
,向前走了![]() 米到达
米到达![]() 处,再沿着坡度为
处,再沿着坡度为![]() ,长度为
,长度为![]() 米台阶到达
米台阶到达![]() 处,测得轨道与大楼连接处顶端
处,测得轨道与大楼连接处顶端![]() 的仰角为
的仰角为![]() ,已知小明的身高为
,已知小明的身高为![]() 米,则
米,则![]() 的高度约为( )米(精确到
的高度约为( )米(精确到![]() ,参考数据:
,参考数据:![]() ,
,![]() ,
,![]() )
)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知双曲线y=![]() (k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(﹣8,4),则△AOC的面积为( )
(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(﹣8,4),则△AOC的面积为( )
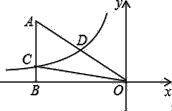
A. 6 B. 12 C. 18 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A、B的坐标分别为(﹣5,0)、(﹣2,0).点P在抛物线y=﹣2x2+4x+8上,设点P的横坐标为m.当0≤m≤3时,△PAB的面积S的取值范围是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
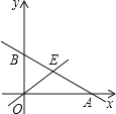
【题目】如图,直线y=-![]() x+b与x轴交于点A,与y轴交于点B,与直线y=x交于点E,点E的横坐标为3.
x+b与x轴交于点A,与y轴交于点B,与直线y=x交于点E,点E的横坐标为3.
(1)求点E的坐标和b的值;
(2)在x轴上有点P(m,0),过点P作x轴的垂线,与直线y=-![]() x+b交于点C,与直线y=x交于点D.若CD≤4,求m的取值范围.
x+b交于点C,与直线y=x交于点D.若CD≤4,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com