
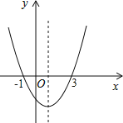
【题目】如图,二次函数y=ax2+bx+c的图象经过(﹣1,0)(3,0)两点,给出的下列6个结论:
①ab<0;
②方程ax2+bx+c=0的根为x1=﹣1,x2=3;
③4a+2b+c<0;
④当x>1时,y随x值的增大而增大;
⑤当y>0时,﹣1<x<3;
⑥3a+2c<0.
其中不正确的有_____.
【答案】⑤
【解析】
①由图象可知,a>0,b<0,则问题可解;②根据图象与x轴交点,问题可解;③由图象可知,当x=2时,对应的点在x轴下方,x=2时,函数值为负;④由图象可知,抛物线对称轴为直线x=1,当x>1时,y随x值的增大而增大;⑤由图象可知,当y>0时,对应x>3或x<-1;⑥根据对称轴找到ab之间关系,再代入a﹣b+c=0,问题可解.综上即可得出结论.
解:①∵抛物线开口向上,对称轴在y轴右侧,与y轴交于负半轴,
∴a>0,﹣![]() >0,c<0,
>0,c<0,
∴b<0,
∴ab<0,说法①正确;
②二次函数y=ax2+bx+c的图象经过(﹣1,0)(3,0)两点,
∴方程ax2+bx+c=0的根为x1=﹣1,x2=3,说法②正确;
③∵当x=2时,函数y<0,
∴4a+2b+c<0,说法③正确;
④∵抛物线与x轴交于(﹣1,0)、(3,0)两点,
∴抛物线的对称轴为直线x=1,
∵图象开口向上,
∴当x>1时,y随x值的增大而增大,说法④正确;
⑤∵抛物线与x轴交于(﹣1,0)、(3,0)两点,且图象开口向上,
∴当y<0时,﹣1<x<3,说法⑤错误;
⑥∵当x=﹣1时,y=0,
∴a﹣b+c=0,
∴抛物线的对称轴为直线x=1=﹣![]() ,
,
∴b=﹣2a,
∴3a+c=0,
∵c<0,
∴3a+2c<0,说法⑥正确.
故答案为⑤.


科目:初中数学 来源: 题型:
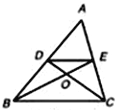
【题目】如图,在△ABC中,中线BE,CD相交于点O,连接DE,下列结论: ①![]() =
=![]() ; ②
; ②![]() =
=![]() ;③
;③![]() =
=![]() ;④
;④![]() =
=![]() .其中正确的个数有( )
.其中正确的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
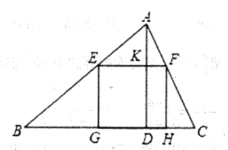
【题目】一块材料的形状是锐角三角形ABC,边BC=120mm,高4D=80mm, .把它加工成正方形零件如图1,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(1)求证:![]() ;
;
(2)求这个正方形零件的边长;
查看答案和解析>>
科目:初中数学 来源: 题型:
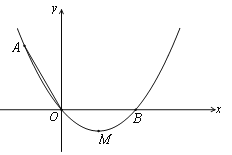
【题目】如图,在平面直角坐标系xOy中,顶点为M的抛物线![]() 经过点A和x轴正半轴上的点B,AO=OB=2,∠AOB=1200.
经过点A和x轴正半轴上的点B,AO=OB=2,∠AOB=1200.
(1)求这条抛物线的表达式;
(2)连接OM,求∠AOM的大小;
(3)如果点C在x轴上,且△ABC与△AOM相似,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 、
、![]() 两组卡片共
两组卡片共![]() 张,
张,![]() 中三张分别写有数字
中三张分别写有数字![]() ,
,![]() ,
,![]() ,
,![]() 中两张分别写有
中两张分别写有![]() ,
,![]() .它们除了数字外没有任何区别.
.它们除了数字外没有任何区别.
![]() 随机地从
随机地从![]() 中抽取一张,求抽到数字为
中抽取一张,求抽到数字为![]() 的概率;
的概率;
![]() 随机地分别从
随机地分别从![]() 、
、![]() 中各抽取一张,请你用画树状图或列表的方法表示所有等可能的结果,现制定这样一个游戏规则:若选出的两数之积为
中各抽取一张,请你用画树状图或列表的方法表示所有等可能的结果,现制定这样一个游戏规则:若选出的两数之积为![]() 的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么?
的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么?
![]() 如果不公平请你修改游戏规则使游戏规则对甲乙双方公平.
如果不公平请你修改游戏规则使游戏规则对甲乙双方公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,点P为射线BD,CE的交点.
(1)求证:BD=CE;
(2)若AB=2,AD=1,把△ADE绕点A旋转,当∠EAC=90°时,求PB的长;
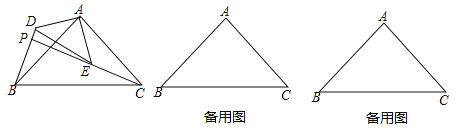
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P为定角∠AOB的平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:(1)PM=PN恒成立;(2)OM+ON的值不变;(3)四边形PMON的面积不变;(4)MN的长不变,其中正确的个数为( )
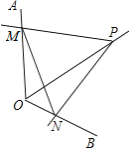
A. 4B. 3C. 2D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一块材料的形状是锐角三角形ABC,边BC=120mm,高4D=80mm, .把它加工成正方形零件如图1,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.

(1)求证:![]() ;
;
(2)求这个正方形零件的边长;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com