
分析 (1)分析所给四组的勾股数:3、4、5;5、12、13;7、24、25;9、40、41;可得下一组一组勾股数:11,60,61;
(2)根据所提供的例子发现股是勾的平方减去1的二分之一,弦是勾的平方加1的二分之一.
解答 解:(1)11,60,61;
(2)后两个数表示为$\frac{{{n^2}-1}}{2}$和$\frac{{{n^2}+1}}{2}$,
∵${n^2}+{(\frac{{{n^2}-1}}{2})^2}={n^2}+\frac{{{n^4}-2{n^2}+1}}{4}=\frac{{{n^4}+2{n^2}+1}}{4}$,${(\frac{{{n^2}+1}}{2})^2}=\frac{{{n^4}+2{n^2}+1}}{4}$,
∴${n^2}+{(\frac{{{n^2}-1}}{2})^2}={(\frac{{{n^2}+1}}{2})^2}$.
又∵n≥3,且n为奇数,
∴由n,$\frac{{{n^2}-1}}{2}$,$\frac{{{n^2}+1}}{2}$三个数组成的数是勾股数.
故答案为:11,60,61.
点评 本题属规律性题目,考查的是勾股数之间的关系,根据题目中所给的勾股数及关系式进行猜想、证明即可.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:填空题
| 地区类别 | 首小时内 | 首小时外 |
| 一类 | 2.5元/15分钟 | 3.75元/15分钟 |
| 二类 | 1.5元/15分钟 | 2.25元/15分钟 |
| 三类 | 0.5元/15分钟 | 0.75元/15分钟 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
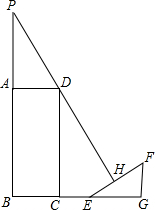 如图,一侧面为矩形的建筑物ABCD,AP为建筑物上一灯杆(垂直于地面),夜晚灯杆顶端灯亮时,EH段是建筑物在斜坡EF上的影子.己知BC=8米,AP=12米,CE=6米,斜坡EF的坡角∠FEG=30°,EH=4米,且B,C,E,G在同一水平线上,题中涉及的各点均在同一平面内,求建筑物的高度AB(结果保留根号).
如图,一侧面为矩形的建筑物ABCD,AP为建筑物上一灯杆(垂直于地面),夜晚灯杆顶端灯亮时,EH段是建筑物在斜坡EF上的影子.己知BC=8米,AP=12米,CE=6米,斜坡EF的坡角∠FEG=30°,EH=4米,且B,C,E,G在同一水平线上,题中涉及的各点均在同一平面内,求建筑物的高度AB(结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
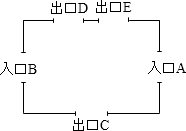 某奥体中心的构造如图所示,其东、西面各有一个入口A、B,南面为出口C,北面分别有两个出口D、E.聪聪若任选一个入口进入,再任选一个出口离开,那么他从入口A进入并从北面出口离开的概率为( )
某奥体中心的构造如图所示,其东、西面各有一个入口A、B,南面为出口C,北面分别有两个出口D、E.聪聪若任选一个入口进入,再任选一个出口离开,那么他从入口A进入并从北面出口离开的概率为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 12 | C. | 16 | D. | 21 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
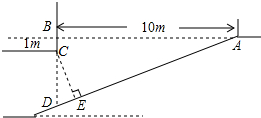 近年来,有私家车的业主越来越多,某小区为解决“停车难”问题,拟建造一个地下停车库.如图是该地下停车库坡道入口的设计示意图,其中水平线AB=10m,BD⊥AB,∠BAD=20°,点C在BD上,BC=1m.根据规定,地下停车库坡道入口上方要张贴限高标志,以提醒驾驶员所驾车辆能否安全驶入.李建认为CD的长度就是限制的高度,而孙杰认为应该以CE的长度作为限制的高度.李建和孙杰谁说的对?请你判断并计算出限制高度.(结果精确到0.1m,参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
近年来,有私家车的业主越来越多,某小区为解决“停车难”问题,拟建造一个地下停车库.如图是该地下停车库坡道入口的设计示意图,其中水平线AB=10m,BD⊥AB,∠BAD=20°,点C在BD上,BC=1m.根据规定,地下停车库坡道入口上方要张贴限高标志,以提醒驾驶员所驾车辆能否安全驶入.李建认为CD的长度就是限制的高度,而孙杰认为应该以CE的长度作为限制的高度.李建和孙杰谁说的对?请你判断并计算出限制高度.(结果精确到0.1m,参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
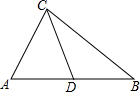 如图,△ABC中,点D在线段AB上,且△ABC∽△ACD,则下列结论一定正确的是( )
如图,△ABC中,点D在线段AB上,且△ABC∽△ACD,则下列结论一定正确的是( )| A. | AC2=AB•AD | B. | AC2=BC•AD | C. | AC•CD=AB•AD | D. | AC•CD=CD•BD |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com