
【题目】如图,AB∥CD, ∠F=90°,则∠1、∠2、∠3间的关系正确的是( )
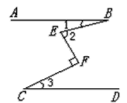
A.∠2=∠1+∠3B.∠1+∠2+∠3=90°
C.∠2+∠3-∠1=90°D.∠1+∠3-∠2=90°
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】为了了解某校九年级全体男生![]() 米跑步的成绩,随机抽取了部分男生进行测试.并将测试成绩分为
米跑步的成绩,随机抽取了部分男生进行测试.并将测试成绩分为![]() 四个成绩,绘制了如下不完整的统计图表.
四个成绩,绘制了如下不完整的统计图表.
成绩等级频数分布表
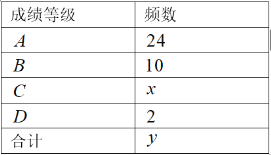
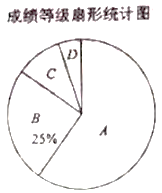
根据图表信息解答下列问题:
![]() 填空:
填空:![]() _____,
_____,![]() _____,扇形统计图中表示
_____,扇形统计图中表示![]() 的扇形的圆心角度数为____度;
的扇形的圆心角度数为____度;
![]() 甲、乙、丙是
甲、乙、丙是![]() 等级中的
等级中的![]() 名学生.学习决定从这
名学生.学习决定从这![]() 名学生中随机抽取
名学生中随机抽取![]() 名来介绍体育锻炼经验,用列表法或画树状图法,求同时抽到甲、乙
名来介绍体育锻炼经验,用列表法或画树状图法,求同时抽到甲、乙![]() 学生的概率.
学生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,四边形ABCD中,AC⊥BD于点O,AO=CO=4,BO=DO=3,点P为线段AC上的一个动点.过点P分别作PM⊥AD于点M,作PN⊥DC于点N. 连接PB,在点P运动过程中,PM+PN+PB的最小值等于_________ .
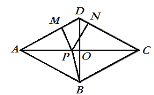
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察以下等式:
第1个等式:![]() ; 第2个等式:
; 第2个等式:![]() ;
;
第3个等式:![]() ;第4个等式:
;第4个等式:![]() ;…
;…
按照以上规律,解决下列问题:
(1)写出第5个等式:_______________
(2)写出你猜想的第n个等式:________________________(用含n的等式表示),并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,“圆材埋壁”是我国古代著名的数学著作《九章算术》中的一个问题,“今有圆材,埋在壁中,不知大小,以锯锯之,深两寸,锯道长八寸,问径几何?”用现代的数学语言表述是:“![]() 为
为![]() 的直径,弦
的直径,弦![]() ,垂足为点
,垂足为点![]() ,
,![]() 寸,
寸,![]() 寸,求直径
寸,求直径![]() 的长?”依题意
的长?”依题意![]() 的长为( )
的长为( )
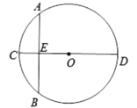
A.6寸B.8寸C.10寸D.12寸
查看答案和解析>>
科目:初中数学 来源: 题型:
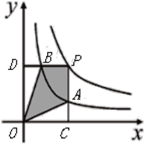
【题目】已知,反比例函数![]() 和
和![]() 的部分图象如图所示,点P在
的部分图象如图所示,点P在![]() 上,PC垂直x轴于点C,交
上,PC垂直x轴于点C,交![]() 于点A(2,1),PD垂直y轴于点D,交
于点A(2,1),PD垂直y轴于点D,交![]() 于点B,连接OA,OB.
于点B,连接OA,OB.
(1)求B点和P点的坐标;
(2)求四边形AOBP的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】袋中有四张卡片,其中两张红色卡片![]() ,标号分别为
,标号分别为![]() ;两张蓝色卡片
;两张蓝色卡片![]() ,标号分别为
,标号分别为![]() .
.
(1)从以上四张卡片中任取两张,求这两张卡片颜色不同且标号之和小于![]() 的概率;
的概率;
(2)向袋中再放入一张绿色卡片![]() ,标号记为
,标号记为![]() ,从这五张卡片中任取两张,求这两张卡片颜色不同且标号之和小于
,从这五张卡片中任取两张,求这两张卡片颜色不同且标号之和小于![]() 的概率.
的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
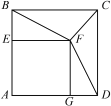
【题目】如图,正方形AEFG的顶点E、G在正方形ABCD的边AB、AD上,连接BF、DF.
![]() (1)求证:BF=DF;
(1)求证:BF=DF;
(2)连接CF,请直接写出![]() 的值为__________(不必写出计算过程).
的值为__________(不必写出计算过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在线段BD上,在BD的同侧作等腰Rt△ABC和等腰Rt△ADE,其中∠ABC=∠AED=90°,CD与BE、AE分别交于点P、M.对于下列结论:①△CAM∽△DEM;②CD=2BE;③MPMD=MAME;④2CB2=CPCM.其中正确的是( )
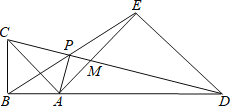
A. ①②B. ①②③C. ①②③④D. ①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com