
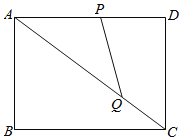
【题目】如图,四边形ABCD是矩形,AB=6,BC=8,点P从A出发在线段AD上以1个单位/秒向点D运动,点Q同时从点C出发,以1个单位/秒的速度向点A运动,当点P到达点D时,点Q也随之停止运动.
(1)设△APQ的面积为S,点P的运行时间为t,求S与t的函数关系式;
(2)t取几时S的值最大,最大值是多少?
(3)当t为何值时,△APQ是等腰三角形?
【答案】(1)S=﹣![]() t2+3t(0<t≤8);(2)当t=5时,△APQ的面积S取得最大值,为
t2+3t(0<t≤8);(2)当t=5时,△APQ的面积S取得最大值,为![]() ;(3)当t=5或t=
;(3)当t=5或t=![]() 或t=
或t=![]() 时,△APQ是等腰三角形.
时,△APQ是等腰三角形.
【解析】
(1)利用sin∠ACB=![]() ,得出sin∠PAQ=
,得出sin∠PAQ=![]() ,即可得出QF=AQsin∠PAQ=
,即可得出QF=AQsin∠PAQ=![]() (10-t),进而表示出△APQ的面积为S;
(10-t),进而表示出△APQ的面积为S;
(2)利用二次函数最值求法运用配方法求出,得出最值;
(3)根据当AP=AQ时和当PA=PQ时当QA=QP时,分别得出t的值.
(1)在△ABC中,∵AB=6,BC=8,∠ABC=90°,
根据勾股定理得AC=10,
∴sin∠ACB=![]() ,同法可得sin∠PAQ=
,同法可得sin∠PAQ=![]() ,
,
过点Q作QF⊥AD于点F,
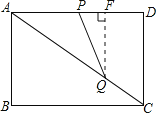
在Rt△AQF中,
∵AQ=10﹣t,
∴QF=AQsin∠PAQ=![]() (10﹣t),
(10﹣t),
∴S=![]() ×t×
×t×![]() (10﹣t),
(10﹣t),
即S=﹣![]() t2+3t(0<t≤8);
t2+3t(0<t≤8);
(2)∵S=﹣![]() (t2﹣10t+25)+
(t2﹣10t+25)+![]() =﹣
=﹣![]() (t﹣5)2+
(t﹣5)2+![]() ,
,
当t=5时,△APQ的面积S取得最大值,为![]() ;
;
(3)△APQ是等腰三角形,
①当AP=AQ时,
t=10﹣t,
则t=5,
②当PA=PQ时,作PE⊥AQ于E
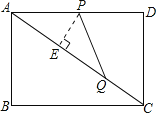
∵cos∠OAQ=![]() ,则AE=
,则AE=![]() t,
t,
∴AQ=![]() t,
t,
∴t+![]() t=10,
t=10,
∴t=![]() ,
,
③当QA=QP时,作QF⊥AD于点F,
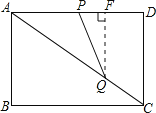
∴AF=![]() (10﹣t),
(10﹣t),
∴![]() (10﹣t)=t,
(10﹣t)=t,
∴t=![]() ,
,
综上所述,当t=5或t=![]() 或t=
或t=![]() 时,△APQ是等腰三角形.
时,△APQ是等腰三角形.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形OABC为矩形,直线y=kx+b交BC于点E(1,m),交AB于点F(4,![]() ),反比例函数y=
),反比例函数y=![]() (x>0)的图象经过点E,F.
(x>0)的图象经过点E,F.
(1)求反比例函数及一次函数解析式;
(2)点P是线段EF上一点,连接PO、PA,若△POA的面积等于△EBF的面积,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按《航空障碍灯(MH/T6012﹣1999)》的要求,为保障飞机夜间飞行的安全,在高度为45米至105米的建筑上必须安装中光强航空障碍灯(AviationObstructionlight).中光强航空障碍灯是以规律性的固定模式闪光.在下图中你可以看到某一种中光强航空障碍灯的闪光模式,灯的亮暗呈规律性交替变化,那么在一个连续的10秒内,该航空障碍灯处于亮的状态的时间总和最长可达__秒.
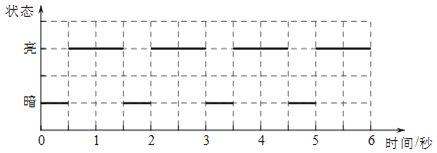
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解初一同学们参加学校社团的情况,某班同学随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表.其中A:英语演讲社团,B:语文阅读社团,C:数学思维训练社团,D:书法社团,E:天文社团.统计后知道:被调查的同学中数学思维训练社团的学生数是书法社团学生数的1.5倍.
各组人数统计表
组别 | 人数 |
A | 4 |
B | 6 |
C | a |
D | b |
E | 10 |
请根据以上图表,解答下列问题:
(1)填空:这次被调查的同学共有____人,m=____;
(2)求扇形统计图中扇形D的圆心角度数;
(3)该校共有1000人,请估计参加书法社团的人数.
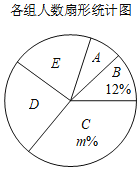
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年5月份,十八中九年级学生参加了中考体育模拟考试,为了了解该校九年级(1)班同学的中考体育情况,对全班学生的中考体育成绩进行了统计,并绘制以下不完整的频数分布表和扇形统计图,根据图表中的信息解答下列问题:
分组 | 分数段(分)) | 频数 |
A | 26≤x<31 | 2 |
B | 31≤x<36 | 5 |
C | 36≤x<41 | 15 |
D | 41≤x<46 | m |
E | 46≤x<51 | 10 |
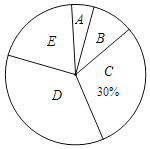
(1)求全班学生人数和m的值.
(2)求扇形统计图中的E对应的扇形圆心角的度数;
(3)该班中考体育成绩满分共有3人,其中男生2人,女生1人,现需从这3人中随机选取2人到八年级进行经验交流,请用“列表法”或“画树状图法”求出恰好选到一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校积极开展中学生社会实践活动,决定成立文明宣传、环境保护、交通监督三个志愿者队伍,每名学生最多选择一个队伍,为了了解学生的选择意向,随机抽取A,B,C,D四个班,共200名学生进行调查.将调查得到的数据进行整理,绘制成如下统计图(不完整)
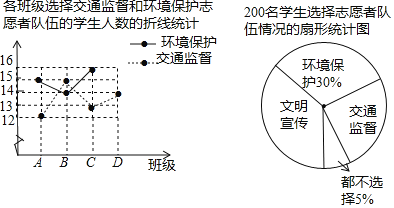
(1)求扇形统计图中交通监督所在扇形的圆心角度数;
(2)求D班选择环境保护的学生人数,并补全折线统计图;(温馨提示:请画在答题卷相对应的图上)
(3)若该校共有学生2500人,试估计该校选择文明宣传的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
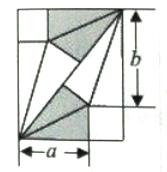
【题目】我国古代数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式,后人借助这种分割方法所得的图形证明了勾股定理,如图所示的长方形由两个这样的图形拼成,若![]() ,
,![]() ,则该长方形的面积为__________.
,则该长方形的面积为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电脑公司准备每周(按120个工时计算)组装三种型号的电脑360台,组装这些电脑每台所需工时和每台产值如下表.
电脑型号 | ① | ② | ③ |
工时(个) |
|
|
|
产值(万元) | 0.4 | 0.3 | 0.2 |
(1)如果每周准备组装100台型号③电脑,那么每周应组装型号①、②电脑各几台?
(2)如果一周产值定为10万元,那么这周应组装型号①、②、③电脑各几台?
(3)若一周型号③电脑至少组装20台,一周产值记为w,试直接写出w的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 三个顶点的坐标分别为
三个顶点的坐标分别为![]() ,
,![]() ,
,![]() ,将
,将![]() 绕原点顺时针旋转
绕原点顺时针旋转![]() 得
得![]() ,
,![]() 与
与![]() 关于
关于![]() 轴对称.
轴对称.
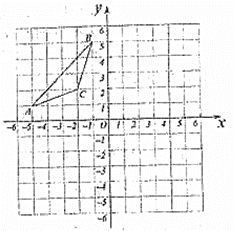
(1)画出![]() 和
和![]() ;
;
(2)![]() ______;
______;
(3)![]() 与
与![]() 组成的图形是否是轴对称图形?若是轴对称图形,请直接写出对称轴所在的直线解析式.
组成的图形是否是轴对称图形?若是轴对称图形,请直接写出对称轴所在的直线解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com