
分析 (1)先把a、b、c对应的值写出来,然后算出△,判断方程根的情况,从而可以求出原方程的根;
(2)先对原方程变形化为一般形式,然后根据公式法解方程即可.
解答 解:(1)x2+3x+1=0,
a=1,b=3,c=1,
△=b2-4ac=32-4×1×1=9-4=5>0,
方程有两个不相等的实数根,
x=$\frac{-3±\sqrt{5}}{2×1}=\frac{-3±\sqrt{5}}{2}$
即${x}_{1}=\frac{-3-\sqrt{5}}{2},{x}_{2}=\frac{-3+\sqrt{5}}{2}$.
(2)$\sqrt{2}$x2-4x=4$\sqrt{2}$
移项,得
$\sqrt{2}{x}^{2}-4x-4\sqrt{2}=0$,
$a=\sqrt{2},b=-4,c=-4\sqrt{2}$,
$△={b}^{2}-4ac=(-4)^{2}-4×\sqrt{2}×(-4\sqrt{2})$=16+32=48>0,
方程有两个不相等的实数根,
x=$\frac{4±\sqrt{48}}{2×\sqrt{2}}=\frac{4±4\sqrt{3}}{2\sqrt{2}}=\sqrt{2}±\sqrt{6}$,
即${x}_{1}=\sqrt{2}-\sqrt{6},{x}_{2}=\sqrt{2}+\sqrt{6}$.
点评 本题考查解一元二次方程---公式法,解题的关键是明确解方程公式法的解答过程.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
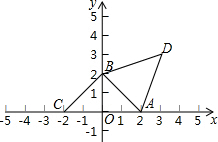 如图,在平面直角坐标系xOy中,A,B两点分别在x轴、y轴的正半轴上,OA=OB=2.
如图,在平面直角坐标系xOy中,A,B两点分别在x轴、y轴的正半轴上,OA=OB=2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.0×109美元 | B. | 1.0×1010美元 | C. | 1.0×1011美元 | D. | 1.0×1012美元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com