
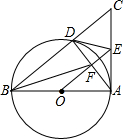
 如图,Rt△ABC中,∠BAC=90°,以AB为直径作⊙O交BC于点D,OE∥BC交AC于点E,连接AD,交OE于点F,连接DE.
如图,Rt△ABC中,∠BAC=90°,以AB为直径作⊙O交BC于点D,OE∥BC交AC于点E,连接AD,交OE于点F,连接DE.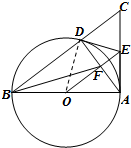 答:(1)DE与⊙O相切.
答:(1)DE与⊙O相切.| 32 |
| 5 |
| 24 |
| 5 |
| 1 |
| 2 |
| 12 |
| 5 |
| BD2+DF2 |
(
|
4
| ||
| 5 |
4
| ||
| 5 |


科目:初中数学 来源: 题型:
 为了增强体质并迎接即将到来的体育中考,全校学生积极参加体育锻炼,学校教务处对学生锻炼时间做了一抽样调查,记录了部分学生锻炼时间如下:
为了增强体质并迎接即将到来的体育中考,全校学生积极参加体育锻炼,学校教务处对学生锻炼时间做了一抽样调查,记录了部分学生锻炼时间如下:| 时间分组(分钟) | 频数(人数) | 频率 |
| 0≤t<15 | 10 | 0.2 |
| 15≤t<30 | 0.4 | |
| 30≤t<45 | 10 | 0.2 |
| 45≤t<60 | 0.1 | |
| 60≤t<75 | 5 | |
| 合计 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
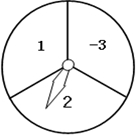 如图转盘,分成三个相同的扇形,3个扇形分别标有数字1、2、-3,指针位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置,并相应得到一个数(指针指向两个扇形的交线时,重新转动转盘).
如图转盘,分成三个相同的扇形,3个扇形分别标有数字1、2、-3,指针位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置,并相应得到一个数(指针指向两个扇形的交线时,重新转动转盘).查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 12 |
| 1 |
| 15 |
| 1 |
| 10 |
| 1 |
| 12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com