
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃНЉx2Љ2x+cЕФОЙ§DЃЈЉ2ЃЌ3ЃЉЃЌгыxжсНЛгкAЁЂBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЁЂгыyжсНЛгкЕуCЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФБэДяЪНКЭAЁЂBСНЕузјБъЃЛ
ЃЈ2ЃЉдкХзЮяЯпЕФЖдГЦжсЩЯгавЛЕуPЃЌЪЙЕУЁЯOAPЃНЁЯBCOЃЌЧѓЕуPЕФзјБъЃЛ
ЃЈ3ЃЉЕуMдкХзЮяЯпЩЯЃЌЕуNдкХзЮяЯпЖдГЦжсЩЯЃЎ
ЂйЕБЁЯACMЃН90ЁуЪБЃЌЧѓЕуMЕФзјБъЃЛ
ЂкЪЧЗёДцдкетбљЕФЕуMгыЕуNЃЌЪЙвдMЁЂNЁЂAЁЂCЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃПШєДцдкЃЌЧыжБНгаДГіЕуMЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
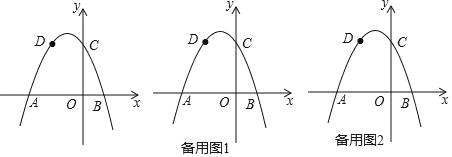
ЁОД№АИЁПЃЈ1ЃЉyЃНЉx2Љ2x+3ЃЌAЃЈЉ3ЃЌ0ЃЉЃЌBЃЈ1ЃЌ0ЃЉЃЈ2ЃЉP1ЃЈЉ1ЃЌ![]() ЃЉЃЛP2ЃЈЉ1ЃЌЉ
ЃЉЃЛP2ЃЈЉ1ЃЌЉ![]() ЃЉЃЈ3ЃЉM1ЃЈЉ2ЃЌ3ЃЉЃЌM2ЃЈЉ4ЃЌЉ5ЃЉЃЌM3ЃЈ2ЃЌЉ5ЃЉ
ЃЉЃЈ3ЃЉM1ЃЈЉ2ЃЌ3ЃЉЃЌM2ЃЈЉ4ЃЌЉ5ЃЉЃЌM3ЃЈ2ЃЌЉ5ЃЉ
ЁОНтЮіЁП
ЃЈ1ЃЉНЋЕуDДњШыКЏЪ§НтЮіЪНЧѓГіc,НјЖјБэЪОГіЖўДЮКЏЪ§ЕФвЛАуЪНЃКyЃНЉx2Љ2x+3ЃЌСюy=0МДПЩЧѓГіA,BЕФзјБъЃЛ
ЃЈ2ЃЉЧѓГіЖўДЮКЏЪ§ЕФЖдГЦжс,НјЖјЧѓГіAH=2, CЃЈ0ЃЌ3ЃЉЃЌЕБЕуPдкxжсЕФЩЯЗНЪБЃЌЩшХзЮяЯпЕФЖдГЦжсгыxжсНЛгкЕуHЃЌвзжЄЁїAHPЁзЁїCOBЃЌЕУ![]() ЃЌМДПЩЧѓГіЕуP1ЃЈЉ1ЃЌ
ЃЌМДПЩЧѓГіЕуP1ЃЈЉ1ЃЌ![]() ЃЉЃЛЕБЕуPдкxжсЕФЯТЗНЪБЃЌМДгыЕуP1ЙигкxжсЖдГЦЪБЃЌЕуP2ЃЈЉ1ЃЌЉ
ЃЉЃЛЕБЕуPдкxжсЕФЯТЗНЪБЃЌМДгыЕуP1ЙигкxжсЖдГЦЪБЃЌЕуP2ЃЈЉ1ЃЌЉ![]() ЃЉЃЛ
ЃЉЃЛ
ЃЈ3ЃЉЂйЙ§ЕуMзїMIЁЭyжсЃЌДЙзуЮЊIЃЌгЩЃЈ2ЃЉжЊЃКAOЃНCOЃЌдђЁЯACOЃНЁЯCAOЃН45ЁуЃЌРћгУЕШбќжБНЧШ§НЧаЮаджЪЕУMIЃНCIЃЌЩшMЃЈxЃЌЉx+3ЃЉЃЌевЕНЕШСПЙиЯЕЉx2Љ2x+3ЃНЉx+3ЃЌМДПЩЧѓГіMЃЈЉ1ЃЌ4ЃЉЃЛЂкЩшГіM,NЕФзјБъ,ЗжБ№ЧѓГіЖдНЧЯпЕФжаЕу,РћгУЦНааЫФБпаЮЕФЖдНЧЯпЛЅЯрЦНЗжетвЛаджЪНЈСЂЗНГЬзщ,ЧѓНтМДПЩ,МћЯъНт.
ЃЈ1ЃЉЁпХзЮяЯпyЃНЉx2Љ2x+cЕФОЙ§DЃЈЉ2ЃЌ3ЃЉЃЌ
ЁрЉ4+4+cЃН3ЃЌ
НтЕУЃКcЃН3ЃЌ
МДХзЮяЯпЕФБэДяЪНЮЊЃКyЃНЉx2Љ2x+3ЃЌ
ЩшyЃН0ЃЌдђ0ЃНЉx2Љ2x+3ЃЌ
НтЕУЃКx1ЃНЉ3ЃЌx2ЃН1ЃЌ
ЁпЕуAдкЕуBЕФзѓВрЃЌ
ЁрAЃЈЉ3ЃЌ0ЃЉЃЌBЃЈ1ЃЌ0ЃЉЃЛ
ЃЈ2ЃЉЁпyЃНЉx2Љ2x+3ЃНЉЃЈx+1ЃЉ2+4ЃЌ
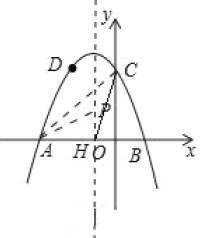
ЁрХзЮяЯпЕФЖдГЦжсЮЊжБЯпxЃНЉ1ЃЌСюХзЮяЯпЖдГЦжсКЭxжсНЛгкЕуH,
ЁрAHЃН2ЃЌСюxЃН0ЃЌдђyЃНЉx2Љ2x+3ЃН3ЃЌ
МДЕуCЃЈ0ЃЌ3ЃЉЃЌ
ЕБЕуPдкxжсЕФЩЯЗНЪБЃЌЩшХзЮяЯпЕФЖдГЦжсlгыxжсНЛгкЕуHЃЌ
ЁпЁЯOAPЃНЁЯBCOЃЌЁЯAHPЃНЁЯCOBЃН90ЁуЃЌ
ЁрЁїAHPЁзЁїCOBЃЌ
Ёр![]() ЃЌ
ЃЌ
МД![]() ЃЌ
ЃЌ
НтЕУЃКPHЃН![]() ЃЌ
ЃЌ
ЁрЕуP1ЃЈЉ1ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
ЕБЕуPдкxжсЕФЯТЗНЪБЃЌМДгыЕуP1ЙигкxжсЖдГЦЪБЃЌЕуP2ЃЈЉ1ЃЌЉ![]() ЃЉЃЛ
ЃЉЃЛ
злЩЯЫљЪіЃКЕуPЕФзјБъЮЊЃКP1ЃЈЉ1ЃЌ![]() ЃЉЃЛP2ЃЈЉ1ЃЌЉ
ЃЉЃЛP2ЃЈЉ1ЃЌЉ![]() ЃЉЃЛ
ЃЉЃЛ
ЃЈ3ЃЉЂйЙ§ЕуMзїMIЁЭyжсЃЌДЙзуЮЊIЃЌгЩЃЈ2ЃЉжЊЃКAOЃНCOЃЌдђЁЯACOЃНЁЯCAOЃН45ЁуЃЌ
ЁпЁЯACMЃН90ЁуЃЌ
ЁрЁЯMCIЃН45ЁуЃЌ
ЁрMIЃНCIЃЌЩшMЃЈxЃЌЉx+3ЃЉЃЌ
ЁрЉx2Љ2x+3ЃНЉx+3ЃЌ
НтЕУЃКx1ЃНЉ1ЃЌx2ЃН0ЃЈЩсШЅЃЉЃЌ
МДMЃЈЉ1ЃЌ4ЃЉЃЛ
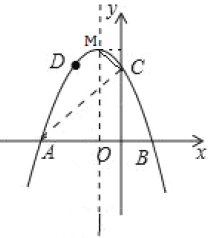
ЂкМйЩшДцдкТњзуЬтвтЕФM,N,ЩшMЃЈm,-m2-2m+3ЃЉ,N(-1,n)гЩЃЈ1ЃЉЃЈ2ЃЉЮЪПЩжЊA(-3,0)C(0,3),
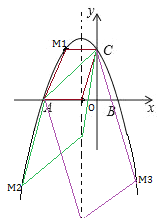
ШєACЮЊЦНааЫФБпаЮЖдНЧЯп,
ЁпЯпЖЮACЕФжаЕузјБъЮЊЃЈ![]() ,
,![]() ЃЉ,ЯпЖЮMNЕФжаЕузјБъЮЊЃЈ
ЃЉ,ЯпЖЮMNЕФжаЕузјБъЮЊЃЈ![]() ЃЉ,
ЃЉ,
Ёр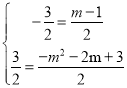
НтЕУЃКm=-2,n=0,дђ-m2-2m+3=3,МДЕуMЕФзјБъЮЊM1ЃЈЉ2ЃЌ3ЃЉЃЌ
ШєANЮЊЦНааЫФБпаЮЖдНЧЯп,ЭЌРэПЩЕУ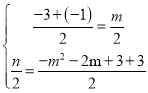
НтЕУЃКm=-4,n=-2,дђ-m2-2m+3=-5,МДЕуMЕФзјБъЮЊM2ЃЈЉ4ЃЌЉ5ЃЉЃЌ
ШєAMЮЊЦНааЫФБпаЮЖдНЧЯп,ЭЌРэПЩЕУ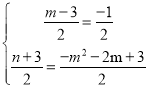
НтЕУЃКm=2,n=-8,дђ-m2-2m+3=-5,МДЕуMЕФзјБъЮЊM3ЃЈ2ЃЌЉ5ЃЉ
ЫљвдMгаШ§ЕуЃЌДЫMЕФзјБъЮЊM1ЃЈЉ2ЃЌ3ЃЉЃЌM2ЃЈЉ4ЃЌЉ5ЃЉЃЌM3ЃЈ2ЃЌЉ5ЃЉ


 гХбЇУћЪІУћЬтЯЕСаД№АИ
гХбЇУћЪІУћЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌAЃЈ4ЃЌ3ЃЉЪЧЗДБШР§КЏЪ§y=![]() дкЕквЛЯѓЯоЭМЯѓЩЯвЛЕуЃЌСЌНгOAЃЌЙ§AзїABЁЮxжсЃЌНиШЁAB=OAЃЈBдкAгвВрЃЉЃЌСЌНгOBЃЌНЛЗДБШР§КЏЪ§y=
дкЕквЛЯѓЯоЭМЯѓЩЯвЛЕуЃЌСЌНгOAЃЌЙ§AзїABЁЮxжсЃЌНиШЁAB=OAЃЈBдкAгвВрЃЉЃЌСЌНгOBЃЌНЛЗДБШР§КЏЪ§y=![]() ЕФЭМЯѓгкЕуPЃЎ
ЕФЭМЯѓгкЕуPЃЎ
ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§y=![]() ЕФБэДяЪНЃЛ
ЕФБэДяЪНЃЛ
ЃЈ2ЃЉЧѓЕуBЕФзјБъЃЛ
ЃЈ3ЃЉЧѓЁїOAPЕФУцЛ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌФГШеЕФЧЎЬСНЙлГБаХЯЂШчБэЃК

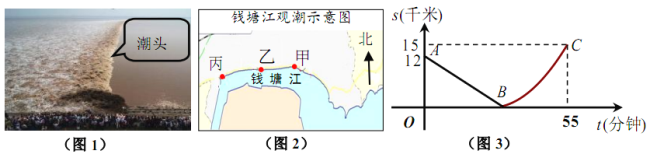
АДЩЯЪіаХЯЂЃЌаЁКьНЋЁАНЛВцГБЁБаЮГЩКѓГБЭЗгыввЕижЎМфЕФОрРы![]() ЃЈЧЇУзЃЉгыЪБМф
ЃЈЧЇУзЃЉгыЪБМф![]() ЃЈЗжжгЃЉЕФКЏЪ§ЙиЯЕгУЭМ3БэЪОЃЌЦфжаЃКЁА11:40ЪБМзЕиЁЎНЛВцГБЁЏЕФГБЭЗРыввЕи12ЧЇУзЁБМЧЮЊЕу
ЃЈЗжжгЃЉЕФКЏЪ§ЙиЯЕгУЭМ3БэЪОЃЌЦфжаЃКЁА11:40ЪБМзЕиЁЎНЛВцГБЁЏЕФГБЭЗРыввЕи12ЧЇУзЁБМЧЮЊЕу![]() ЃЌЕу
ЃЌЕу![]() зјБъЮЊ
зјБъЮЊ![]() ЃЌЧњЯп
ЃЌЧњЯп![]() ПЩгУЖўДЮКЏЪ§
ПЩгУЖўДЮКЏЪ§![]() ЃЈ
ЃЈ![]() ЃЌ
ЃЌ![]() ЪЧГЃЪ§ЃЉПЬЛЃЎ
ЪЧГЃЪ§ЃЉПЬЛЃЎ
ЃЈ1ЃЉЧѓ![]() ЕФжЕЃЌВЂЧѓГіГБЭЗДгМзЕиЕНввЕиЕФЫйЖШЃЛ
ЕФжЕЃЌВЂЧѓГіГБЭЗДгМзЕиЕНввЕиЕФЫйЖШЃЛ
ЃЈ2ЃЉ11:59ЪБЃЌаЁКьЦяЕЅГЕДгввЕиГіЗЂЃЌбиНБпЙЋТЗвд![]() ЧЇУз/ЗжЕФЫйЖШЭљМзЕиЗНЯђШЅПДГБЃЌЮЪЫ§МИЗжжгКѓгыГБЭЗЯргіЃП
ЧЇУз/ЗжЕФЫйЖШЭљМзЕиЗНЯђШЅПДГБЃЌЮЪЫ§МИЗжжгКѓгыГБЭЗЯргіЃП
ЃЈ3ЃЉЯргіКѓЃЌаЁКьСЂМДЕїзЊГЕЭЗЃЌбиНБпЙЋТЗАДГБЭЗЫйЖШгыГБЭЗВЂааЃЌЕЋГБЭЗЙ§ввЕиКѓОљдШМгЫйЃЌЖјЕЅГЕзюИпЫйЖШЮЊ![]() ЧЇУз/ЗжЃЌаЁКьж№НЅТфКѓЃЌЮЪаЁКьгыГБЭЗЯргіЕНТфКѓГБЭЗ1.8ЧЇУзЙВашЖрГЄЪБМфЃПЃЈГБЫЎМгЫйНзЖЮЫйЖШ
ЧЇУз/ЗжЃЌаЁКьж№НЅТфКѓЃЌЮЪаЁКьгыГБЭЗЯргіЕНТфКѓГБЭЗ1.8ЧЇУзЙВашЖрГЄЪБМфЃПЃЈГБЫЎМгЫйНзЖЮЫйЖШ![]() ЃЌ
ЃЌ![]() ЪЧМгЫйЧАЕФЫйЖШЃЉЃЎ
ЪЧМгЫйЧАЕФЫйЖШЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПАб9ИіжЛгабеЩЋВЛЭЌЕФаЁЧђЗжБ№зАШыМзввБћШ§ИіВМДќРяЦфжаМзВМДќРяга3ИіКьЧђЃЌ1ИіАзЧђЃЛввВМДќРяга1ИіКьЧђЃЌ2ИіАзЧђЃЛБћВМДќРяга1ИіКьЧђЃЌ1ИіАзЧђЃЎ
ЃЈ1ЃЉДгМзВМДќжаЫцЛњУўГі1ИіаЁЧђЃЌУўГіЕФаЁЧђЪЧКьЧђЕФИХТЪЪЧЖрЩйЃП
ЃЈ2ЃЉгУСаБэЗЈЛђЛЪїзДЭМЃЌНтОіЯТСаЮЪЬтЃК
ЂйДгМзЁЂввСНИіВМДќжаЫцЛњИїУўГі1ИіаЁЧђЃЌЧѓУўГіЕФСНИіаЁЧђЖМЪЧКьЧђЕФИХТЪЃЛ
ЂкДгМзЁЂввЁЂБћШ§ИіВМДќжаЫцЛњИїУўГі1ИіаЁЧђЃЌЧѓУўГіЕФШ§ИіаЁЧђЪЧвЛКьЖўАзЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
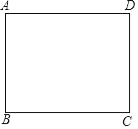
ЁОЬтФПЁПШчЭМЃЌОиаЮжНЦЌABCDЃЌAD=4ЃЌAB=3ЃЌШчЙћЕуEдкБпBCЩЯЃЌНЋжНЦЌбиAEелЕўЃЌЪЙЕуBТфдкЕуFДІЃЌСЊНсFCЃЌЕБЁїEFCЪЧжБНЧШ§НЧаЮЪБЃЌФЧУДBEЕФГЄЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
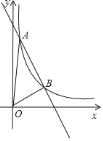
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§y=-2x+8гыЗДБШР§КЏЪ§y=![]() ЃЈxЃО0ЃЉЕФЭМЯѓНЛгкAЃЈmЃЌ6ЃЉЃЌBЃЈ3ЃЌnЃЉСНЕуЃЎ
ЃЈxЃО0ЃЉЕФЭМЯѓНЛгкAЃЈmЃЌ6ЃЉЃЌBЃЈ3ЃЌnЃЉСНЕуЃЎ
ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉИљОнЭМЯѓжБНгаДГіЙигкxЕФВЛЕШЪН-2x+8-![]() ЃО0ЕФНтМЏЃЎ
ЃО0ЕФНтМЏЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЭМЃЌаЁЖЋдкНЬбЇТЅОрЕиУц9УзИпЕФДАПкCДІЃЌВтЕУе§ЧАЗНЦьИЫЖЅВПAЕуЕФбіНЧЮЊ37ЁуЃЌЦьИЫЕзВПBЕуЕФИЉНЧЮЊ45ЁуЃЌЩ§ЦьЪБЃЌЙњЦьЩЯЖЫаќЙвдкОрЕиУц2.25УзДІЃЌШєЙњЦьЫцЙњИшЩљШНШНЩ§Ц№ЃЌВЂдкЙњИшВЅЗХ45УыНсЪјЪБЕНДяЦьИЫЖЅЖЫЃЌдђЙњЦьгІвдЖрЩйУз/УыЕФЫйЖШдШЫйЩЯЩ§ЃПЃЈВЮПМЪ§ОнЃКsin37ЁуЁж0.60ЃЌcos37ЁуЁж0.80ЃЌtan37ЁуЁж0.75ЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌШєИЩИіШЋЕШЕФе§ЮхБпаЮХХГЩЛЗзДЃЌЭМжаЫљЪОЕФЪЧЧА3Иіе§ЮхБпаЮЃЌвЊЭъГЩетвЛдВЛЗЛЙаше§ЮхБпаЮЕФИіЪ§ЮЊЃЈЁЁЁЁЃЉ
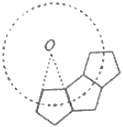
A. 10 B. 9 C. 8 D. 7
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЋСНБпГЄЗжБ№ЪЧ![]() КЭ
КЭ![]() ЕФОиаЮвдЦфвЛБпЫљдкЕФжБЯпЮЊжса§зЊвЛжмЃЌЫљЕУЕФМИКЮЬхЕФВрУцЛ§ЪЧ_____
ЕФОиаЮвдЦфвЛБпЫљдкЕФжБЯпЮЊжса§зЊвЛжмЃЌЫљЕУЕФМИКЮЬхЕФВрУцЛ§ЪЧ_____![]() .
.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com