
���� ��1���ѣ�-x��-y������y=2��x-1��2+3�����ɵõ�����ʽy�䣮
��2������ͼ�ɽ�����⣮
��3�������y3��y4�Ľ���ʽ������ͼ�ɽ�����⣮
��� �⣺��1�����κ���y=2��x-1��2+3������ԭ�����ĶԳƶ��κ�����y��ĺ�������ʽΪy��=-2����x+1��2-3��
��2����ͼ��ͼ���֪�����κ���y��y��ĺ���ֵͬʱ��x���������Сʱ��-1��x��1��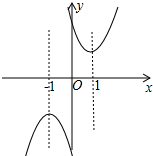
��3�������⣬a2=-1��b1=b2��c1=-c2��
��y3=y1+y2=2b1x��y4=$\frac{1}{2}$��y1-y2��=x2+c1��
�ߺ���y3=y1+y2��ͼ���뺯��y4=$\frac{1}{2}$��y1-y2����ͼ���ڵ㣨1��2����
��b1=1��c1=1��
��y3=2x��y4=x2+1��
����ͼ���֪��y4��y3��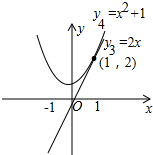 ��
��
���� ���⿼����κ����ۺ��⡢����Ĺؼ����������⣬ѧ�����ú���ͼ�������⣬ѧ��̽������ԭ�����ĶԳƵĶ��κ����Ľ���ʽ������������̽���õ����ɽ�����⣬�����п�ѹ���⣮


 ͬ��������ϰϵ�д�
ͬ��������ϰϵ�д� �ο�ͨ�γ̱�˼ά����������ѵ��ϵ�д�
�ο�ͨ�γ̱�˼ά����������ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������ÿ��С�����εı߳���Ϊ1���߶�AB���߶�EF�Ķ˵����С�����εĶ����ϣ�
��ͼ��������ÿ��С�����εı߳���Ϊ1���߶�AB���߶�EF�Ķ˵����С�����εĶ����ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ�������ο�ƬA�࣬B��ͳ����ο�ƬC�������ţ���Ҫ��A��B��C���Ƭƴһ����Ϊ��a+3b������Ϊ��a+b���ij����Σ�����ҪC�Ƭ��������
��ͼ�������ο�ƬA�࣬B��ͳ����ο�ƬC�������ţ���Ҫ��A��B��C���Ƭƴһ����Ϊ��a+3b������Ϊ��a+b���ij����Σ�����ҪC�Ƭ��������| A�� | 2�� | B�� | 3�� | C�� | 4�� | D�� | 5�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ���������ſ�Ƭ���ֱ��������ο�ƬA��B�ͳ����ο�ƬC����Ƭ��С��ͼ��ʾ�����Ҫƴһ����Ϊ��3a+b������Ϊ��a+2b���Ĵ��Σ�����ҪC�Ƭ7�ţ�
���������ſ�Ƭ���ֱ��������ο�ƬA��B�ͳ����ο�ƬC����Ƭ��С��ͼ��ʾ�����Ҫƴһ����Ϊ��3a+b������Ϊ��a+2b���Ĵ��Σ�����ҪC�Ƭ7�ţ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 4 | C�� | 5 | D�� | 6 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com