
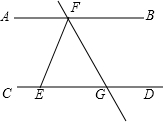
 如图,AB∥CD,∠EFB=2∠DEF,FG平分∠EFB,则∠EGF=60°.
如图,AB∥CD,∠EFB=2∠DEF,FG平分∠EFB,则∠EGF=60°.  名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案科目:初中数学 来源: 题型:选择题
| A. | (-$\frac{5}{4}$x2)(-4ax)2=5a2x4 | B. | x(2x2-x+1)=2x3-x2+1 | ||
| C. | (a+2b)2=a2+2ab+4b2 | D. | (-3m-2n)(-2n+3m)=4n2-9m2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
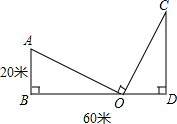 一位同学和妈妈一起逛街时发现了这样一个问题:如图,两座相距60米的大楼,分别从各自楼顶悬挂一条一样的条幅到地面,两条幅拉直后长度相同且他用手里的书测量了一下发现两个条幅互相垂直,最后都固定在地面上同一处,现在这位同学知道其中一座楼高20米,他想了想告诉妈妈他可以在地面上测量出另一座楼的高度,你知道他是怎么做的吗?
一位同学和妈妈一起逛街时发现了这样一个问题:如图,两座相距60米的大楼,分别从各自楼顶悬挂一条一样的条幅到地面,两条幅拉直后长度相同且他用手里的书测量了一下发现两个条幅互相垂直,最后都固定在地面上同一处,现在这位同学知道其中一座楼高20米,他想了想告诉妈妈他可以在地面上测量出另一座楼的高度,你知道他是怎么做的吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 数学实验室:
数学实验室:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com