
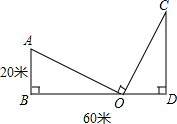
 一位同学和妈妈一起逛街时发现了这样一个问题:如图,两座相距60米的大楼,分别从各自楼顶悬挂一条一样的条幅到地面,两条幅拉直后长度相同且他用手里的书测量了一下发现两个条幅互相垂直,最后都固定在地面上同一处,现在这位同学知道其中一座楼高20米,他想了想告诉妈妈他可以在地面上测量出另一座楼的高度,你知道他是怎么做的吗?
一位同学和妈妈一起逛街时发现了这样一个问题:如图,两座相距60米的大楼,分别从各自楼顶悬挂一条一样的条幅到地面,两条幅拉直后长度相同且他用手里的书测量了一下发现两个条幅互相垂直,最后都固定在地面上同一处,现在这位同学知道其中一座楼高20米,他想了想告诉妈妈他可以在地面上测量出另一座楼的高度,你知道他是怎么做的吗? 分析 根据全等三角形的判定定理AAS证得△ABO≌△ODC,则其对应边相等:AB=OD=20米,OB=CD=40米.
解答  解:如图,AB=20米,BD=60米,OA=OC,AB⊥BD,CD⊥BD,AO⊥CO.
解:如图,AB=20米,BD=60米,OA=OC,AB⊥BD,CD⊥BD,AO⊥CO.
∵AB⊥BD,CD⊥BD,AO⊥CO,
∴∠B=∠D=90°,且∠A=∠COD(同角的余角相等).
在△ABO与△ODC中,
$\left\{\begin{array}{l}{∠B=∠D=90°}\\{∠A=∠COD}\\{OA=OC}\end{array}\right.$,
∴△ABO≌△ODC(AAS),
∴AB=OD=20米,OB=CD,
∴OB=BD-OD=40米,
∴CD=40米.
即另一座楼的高度是40米.
点评 本题考查了全等三角形的应用.用全等寻找下一个全等三角形的条件,全等的性质和判定往往是综合在一起应用的,这需要认真分析题目的已知和求证,分清问题中已知的线段和角与所证明的线段或角之间的联系.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:选择题
| A. | 69.6×104 | B. | 6.96×105 | C. | 6.96×106 | D. | 0.696×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
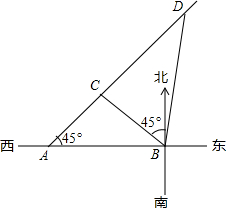 如图,一艘轮船位于灯塔B的正西方向上的A处,且灯塔B到A处的距离为40海里,轮船沿东北方向匀速航行,速度为20海里/时.
如图,一艘轮船位于灯塔B的正西方向上的A处,且灯塔B到A处的距离为40海里,轮船沿东北方向匀速航行,速度为20海里/时.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
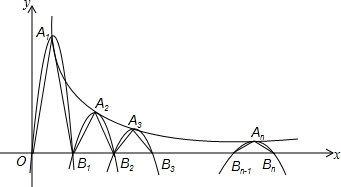 如图,一组抛物线的顶点A1(x1,y1),A2(x2,y2),…An(xn,yn)(n为正整数)依次是反比例函数y=$\frac{9}{x}$图象上的点,第一条抛物线以A1(x1,y1)为顶点且过点O(0,0),B1(2,0),等腰△A1OB1为第一个三角形;第二条抛物线以A2(x2,y2)为顶点且经过点B1(2,0),B2(4,0),等腰△A2B1B2为第二个三角形;…;第n条抛物线以An(xn,yn)为顶点且经过点Bn-1(2n-2,0),B2n(2n,0),等腰△AnBn-1Bn为第n个三角形.
如图,一组抛物线的顶点A1(x1,y1),A2(x2,y2),…An(xn,yn)(n为正整数)依次是反比例函数y=$\frac{9}{x}$图象上的点,第一条抛物线以A1(x1,y1)为顶点且过点O(0,0),B1(2,0),等腰△A1OB1为第一个三角形;第二条抛物线以A2(x2,y2)为顶点且经过点B1(2,0),B2(4,0),等腰△A2B1B2为第二个三角形;…;第n条抛物线以An(xn,yn)为顶点且经过点Bn-1(2n-2,0),B2n(2n,0),等腰△AnBn-1Bn为第n个三角形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com