
分析 (1)因式分解法求解可得;
(2)配方法求解可得.
解答 解:(1)∵(2x-1)2+2(2x-1)=0,
∴(2x-1)(2x+1)=0,
则2x-1=0或2x+1=0,
解得:x=$\frac{1}{2}$或x=-$\frac{1}{2}$;
(2)∵2x2-x=3,
∴x2-$\frac{1}{2}$x=$\frac{3}{2}$,
∴x2-$\frac{1}{2}$x+$\frac{1}{16}$=$\frac{3}{2}$+$\frac{1}{16}$,即(x-$\frac{1}{4}$)2=$\frac{25}{16}$,
则x-$\frac{1}{4}$=±$\frac{5}{4}$,
∴x=$\frac{3}{2}$或x=-$\frac{1}{2}$.
点评 本题主要考查解一元二次方程的基本技能,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,根据不同方程的特点选择合适的、简便的方法是解题的关键.


科目:初中数学 来源: 题型:解答题
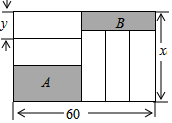 如图,长为60cm,宽为x(cm)的大长方形被分割为7小块,除阴影 A,B外,其余5块是形状、大小完全相同的小长方形,其较短一边长为 y (cm).
如图,长为60cm,宽为x(cm)的大长方形被分割为7小块,除阴影 A,B外,其余5块是形状、大小完全相同的小长方形,其较短一边长为 y (cm).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2016,2017) | B. | (2016,-2017) | C. | (2016,2017) | D. | (-2016,-2017) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知线段AB,根据下列语句画出图形计算:
如图,已知线段AB,根据下列语句画出图形计算:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com