
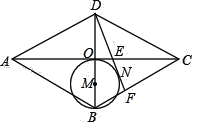
【题目】如图,在菱形ABCD中,对角线AC、BD交于点O,以OB为直径画圆M,过D作⊙M的切线,切点为N,分别交AC、BC于点E、F,已知AE=5,CE=3,则菱形ABCD的面积是( )
A. 24B. 20C. ![]() D.
D. ![]()
科目:初中数学 来源: 题型:
【题目】抛物线![]()
![]() 过点
过点![]() ,顶点为M点.
,顶点为M点.

(1)求该抛物线的解析式;
(2)试判断抛物线上是否存在一点P,使∠POM=90.若不存在,说明理由;若存在,求出P点的坐标;
(3)试判断抛物线上是否存在一点K,使∠OMK=90,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对非负实数x“四舍五入”到个位的值记为< x >,即已知n为正整数,如果n-![]() ≤x<n+
≤x<n+![]() ,那么< x >=n.例如:< 0 >=< 0.48 >=0,< 0.64 >=< 1.493 >=1,< 2 >=2,< 3.5 >=< 4.12 >=4,…则满足方程< x >=
,那么< x >=n.例如:< 0 >=< 0.48 >=0,< 0.64 >=< 1.493 >=1,< 2 >=2,< 3.5 >=< 4.12 >=4,…则满足方程< x >=![]() 的非负实数x的值为____.
的非负实数x的值为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=3x﹣3分别交x轴、y轴于A、B两点,抛物线y=![]() +bx+c经过A、B两点,点C是抛物线与x轴的另一个交点,该抛物线的对称轴与x轴交于点E.
+bx+c经过A、B两点,点C是抛物线与x轴的另一个交点,该抛物线的对称轴与x轴交于点E.
(1)直接写出抛物线的解析式为 ;
(2)以点E为圆心的⊙E与直线AB相切,求⊙E的半径;
(3)连接BC,点P是第三象限内抛物线上的动点,连接PE交线段BC于点D,当△CED为直角三角形时,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
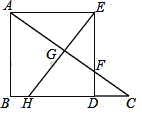
【题目】如图,在Rt△ABC中,∠B=90°,BC>AB,在BC边上取点D,使AB=BD,构造正方形ABDE,DE交AC于点F,作EG⊥AC交AC于点G,交BC于点H.
(1)求证:△AEF≌△EDH.
(2)若AB=3,DH=2DF,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
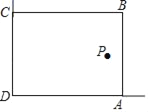
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用32m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
(1)若花园的面积为252m2,求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是17m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(m,m+1),B(m+3,m-1)是反比例函数![]() 与一次函数
与一次函数![]() 的交点.
的交点.
(1)求反比例函数与一次函数的解析式;
(2)请直接写出当反比例函数的函数值不大于一次函数的函数值时,自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
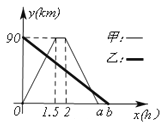
【题目】A、B两地相距90km,甲骑摩托车由A地出发,去B地办事,甲出发的同时,乙骑自行车同时由B地出发沿着同一条道路前往A地,甲办完事后原速返回A地,结果比乙早到0.5小时.甲、乙两人离A地距离y(km)与时间x(h)的函数关系图像如图所示.下列说法:①.a=3.5,b=4;② 甲走的全路程是90km;③乙的平均速度是22.5km/h;.④甲在B地办事停留了0.5小时.其中正确的说法有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
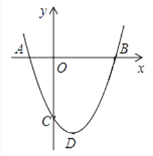
【题目】已知:如图,抛物线的顶点D的坐标为(1,-4),且与y轴交于点C(0,-3).
(1)求该函数的关系式及该抛物线与x轴的交点A,B的坐标.
(2)请直接写出△ABC的外心M的坐标.
(3)点E为该抛物线上一动点,且满足tan∠ABE=![]() tan∠ACB,请求出点E的坐标.
tan∠ACB,请求出点E的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com