
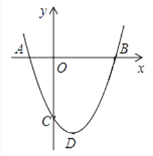
【题目】已知:如图,抛物线的顶点D的坐标为(1,-4),且与y轴交于点C(0,-3).
(1)求该函数的关系式及该抛物线与x轴的交点A,B的坐标.
(2)请直接写出△ABC的外心M的坐标.
(3)点E为该抛物线上一动点,且满足tan∠ABE=![]() tan∠ACB,请求出点E的坐标.
tan∠ACB,请求出点E的坐标.
【答案】(1)![]() ,A(-1,0) B(3,0);(2) (1,-1);(3)(-
,A(-1,0) B(3,0);(2) (1,-1);(3)(-![]() ),(-
),(-![]() ,-
,-![]() ).
).
【解析】
(1)利用顶点式即可解决问题,令y=0,解方程即可得到A、B的坐标;
(2)由外心为三边中垂线的交点,得到外心M在抛物线的对称轴x=1上,设M(1,y),根据MA=MC,用两点间的距离公式列方程,求解即可;
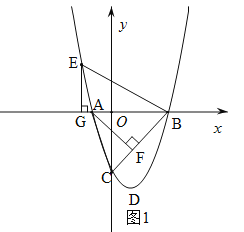
(3)连接AC、BC.过A作AF⊥CB于F.先求出tan∠ACB的值,即可得到tan∠ABE的值.分两种情况讨论:①当E在x轴上方时,如图1,过E作EG⊥x轴于G,连接EB.设E(x,x2-2x-3),则EG= x2-2x-3,GB=3-x,由tan∠ABE=![]() ,列方程求出x的值,即可得到E的坐标;②当E在x轴上方时,如图2,同理可求E的坐标.
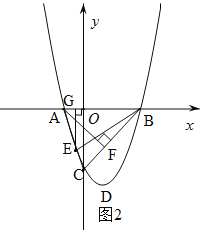
,列方程求出x的值,即可得到E的坐标;②当E在x轴上方时,如图2,同理可求E的坐标.
(1)设抛物线顶点式为y=a(x﹣1)2-4,将C(0,-3)代入得:a-4=-3,解得:a=1,所以抛物线的关系式为:y=(x﹣1)2﹣4=x2-2x-3,令y=0,即:(x﹣1)2﹣4=0,解得:x1=3,x2=﹣1.∴坐标为A(﹣1,0),B(3,0).
(2)∵外心为三边中垂线的交点,∴外心M在抛物线的对称轴x=1上,设M(1,y).
∵MA=MC,∴![]() ,解得:y=-1,∴M(1,-1);
,解得:y=-1,∴M(1,-1);
(3)连接AC、BC.过A作AF⊥CB于F.AB=3-(-1)=4,BC=![]() .
.
∵OB=OC=3,∴∠OBC=45°,∴AF=BF=![]() ,∴CF=BC-BF=
,∴CF=BC-BF=![]() ,∴tan∠ACB=
,∴tan∠ACB=![]() =2,∴tan∠ABE=
=2,∴tan∠ABE=![]() tan∠ACB=
tan∠ACB=![]() ./span>
./span>
分两种情况讨论:①当E在x轴上方时,如图1,过E作EG⊥x轴于G,连接EB.设E(x,x2-2x-3),则EG= x2-2x-3,GB=3-x.
∵tan∠ABE=![]() ,∴
,∴![]() ,∴
,∴![]() ,解得:
,解得:![]() ,
,![]() (舍去),∴x=
(舍去),∴x=![]() ,y= x2-2x-3=
,y= x2-2x-3=![]() ,∴E(
,∴E(![]() ,
,![]() );
);
②当E在x轴上方时,如图2,过E作EG⊥x轴于G,连接EB.设E(x,x2-2x-3),则EG= -x2+2x+3,GB=3-x.
∵tan∠ABE=![]() ,∴
,∴![]() ,∴
,∴![]() ,解得:
,解得:![]() ,
,![]() (舍去),∴x=
(舍去),∴x=![]() ,y= x2-2x-3=
,y= x2-2x-3=![]() ,∴E(
,∴E(![]() ,
,![]() ).
).
综上所述:E的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
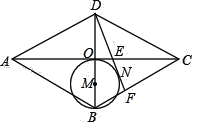
【题目】如图,在菱形ABCD中,对角线AC、BD交于点O,以OB为直径画圆M,过D作⊙M的切线,切点为N,分别交AC、BC于点E、F,已知AE=5,CE=3,则菱形ABCD的面积是( )
A. 24B. 20C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯公司推出①,②两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通讯时间x(分)与费用y(元)之间的函数关系如图所示.
(1)有月租的收费方式是________(填“①”或“②”),月租费是________元;
(2)分别求出①,②两种收费方式中y与自变量x之间的函数表达式;
(3)请你根据用户通讯时间的多少,给出经济实惠的选择建议.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)求证:ΔABC≌△DEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场一种商品的进价为每件30元,售价为每件40元.每天可以销售48件,为尽快减少库存,商场决定降价促销.
(1)若该商品连续两次下调相同的百分率后售价降至每件32.4元,求两次下降的百分率;
(2)经调查,若每降价0.5元,每天可多销售4件,那么每天要想获得510元的利润,每件应降价多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,等边△AOB的边长为6,点C在边OA上,点D在边AB上,且OC=3BD,反比例函数![]() (k≠0)的图象恰好经过点C和点D,则k的值为( )
(k≠0)的图象恰好经过点C和点D,则k的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据扬州市某风景区的旅游信息,![]() 公司组织一批员工到该风景区旅游,支付给旅行社
公司组织一批员工到该风景区旅游,支付给旅行社![]() 元.
元. ![]() 公司参加这次旅游的员工有多少人?
公司参加这次旅游的员工有多少人?
扬州市某风景区旅游信息表
旅游人数 | 收费标准 |
不超过 | 人均收费 |
超过 | 每增加 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com