
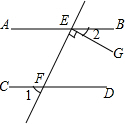
 如图,直线AB∥CD,直线EF与AB、CD分别交于点E、F,EG⊥EF,垂足为E,若∠1=50°,求∠2的度数.
如图,直线AB∥CD,直线EF与AB、CD分别交于点E、F,EG⊥EF,垂足为E,若∠1=50°,求∠2的度数. 科目:初中数学 来源: 题型:解答题
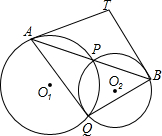 如图,⊙O1与⊙O2相交于P、Q两点,过P点作两圆的割线分别交于⊙O1与⊙O2于A、B,过A、B分别作两圆的切线相交于T,求证:T、A、Q、B四点共圆.
如图,⊙O1与⊙O2相交于P、Q两点,过P点作两圆的割线分别交于⊙O1与⊙O2于A、B,过A、B分别作两圆的切线相交于T,求证:T、A、Q、B四点共圆.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC:∠EOD=1:2,则∠BOD等于( )
如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC:∠EOD=1:2,则∠BOD等于( )| A. | 30° | B. | 36° | C. | 45° | D. | 72° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
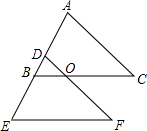 如图所示,△ABC平移后得到△DEF.
如图所示,△ABC平移后得到△DEF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
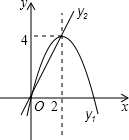 如图,已知抛物线y1=-x2+4x和直线y2=2x.我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.则①当x>4时,M<0;②当x<2时,M随着x增大而增大;③使得M大于4的x值不存在;④若M=2,则x=1,其中正确的有②③(填写序号)
如图,已知抛物线y1=-x2+4x和直线y2=2x.我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.则①当x>4时,M<0;②当x<2时,M随着x增大而增大;③使得M大于4的x值不存在;④若M=2,则x=1,其中正确的有②③(填写序号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com