
����Ŀ��Ϊ�˴���ȫ���������У�ij����Ҫ����һ�����������ڵ����������üס����������ͣ�����������������12�˲�����ɣ���֧���˷ѹ�4 800Ԫ�����ס���������������˶����������ҳ����������Ǽ׳���2������֪�ҳ�ÿ���˷ѱȼ׳���200Ԫ��
(1)�ֱ�����ס�������ÿ�˵��˷ѣ�
(2)���������ü׳�����˶�������������ˣ�
(3)��ͬʱ���üס�����������׳���x�ˣ��ҳ���y�ˣ���������˶�����������x��y��Ϊ��������
�ٵ�x��10ʱ��y�� ����y��10ʱ��x�� ��
���ú�x�Ĵ���ʽ��ʾy��
̽����
(4)��(3)�������£�
���ú�x�Ĵ���ʽ��ʾ���˷�w��
��Ҫ�����˷Ѳ�����4 000Ԫ���׳�������˶����ˣ�
���𰸡���1���ס�������ÿ�˵��˷ѷֱ�Ϊ300Ԫ��100Ԫ����2���������ü׳�����˶�����������18�ˣ���3����16��13��y=36��2x����4����w=100x��3600���ڼ׳��������4�ˣ�
��������
��1����ס�������ÿ�˵��˷ѷֱ�ΪmԪ��nԪ�����������г���Ԫһ�η����飬��⼴�ɣ�
��2���赥�����ü׳�����˶�����������![]() �ˣ��������۳���ʽ���̣���⼴�ɣ�
�ˣ��������۳���ʽ���̣���⼴�ɣ�
��3�����г���ʽ������⼴�ɣ�
�ڸ������⣬�г���ʽ����ת����ʽ���ɣ�
��4���ٽ�ϣ�1���ͣ�3���Ľ��ۣ��г�������ϵʽ���ɣ�
�ڸ��������г�����ʽ����⼴��.
(1)��ס�������ÿ�˵��˷ѷֱ�ΪmԪ��nԪ�������⣬��
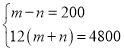 ���
���![]()
�𣺼ס�������ÿ�˵��˷ѷֱ�Ϊ300Ԫ��100Ԫ��
(2)�赥�����ü׳�����˶�����������![]() �ˣ������⣬��
�ˣ������⣬��
![]() ���
���![]()
�����飬![]() ��ԭ���̵Ľ⣬�ҷ������⣮
��ԭ���̵Ľ⣬�ҷ������⣮
�𣺵������ü׳�����˶�����������18�ˣ�
(3)�������⣬��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
�������⣬��![]() ��
��
��y=36��2x��
(4)���ɣ�1���ͣ�3���������˷�Ϊw=300x��100y=300x��100(36��2x) =100x��3600��
�������⣬��100x��3600��4 000��
��x��4��
�𣺼׳��������4�ˣ�


 Сѧ��10���ӿ������100��ϵ�д�
Сѧ��10���ӿ������100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1������A��0��4����Բ��Բ������ΪC��2��0����B�ǵ�һ����Բ���ϵ�һ�㣬��BC��AC��������![]() ����C��B���㣬��x�����һ����ΪD��
����C��B���㣬��x�����һ����ΪD��
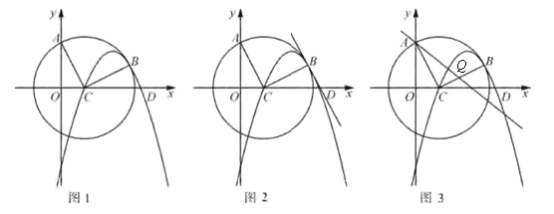
��1����B������Ϊ�� �� ���������ߵı���ʽΪ .
��2����ͼ2����֤��BD//AC��
��3����ͼ3����QΪ�߶�BC��һ�㣬��AQ=5��ֱ��AQ����C�ڵ�P����AP�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
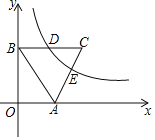
����Ŀ����ͼ����ƽ��ֱ��ϵ�У���A��x���������ϣ���B��y���������ϣ���ABO��30����AB��2����ABΪ���ڵ�һ���������ȱߡ�ABC��������������ͼ��ǡ�þ�����BC���е�D����AC�뷴����������ͼ���ڵ�E��
��1�����������Ľ���ʽ��
��2�����E�ĺ����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
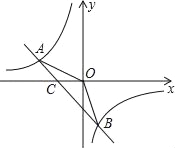
����Ŀ����ͼ����֪A����4��n����B��2����4����һ�κ���y��kx+b��ͼ��ͷ���������y��![]() ��ͼ����������㣮
��ͼ����������㣮
��1������������һ�κ����Ľ���ʽ��
��2����ֱ��AB��x��Ľ���C�����꼰��AOB�������
��3��ֱ��д��һ�κ�����ֵС�ڷ���������ֵ��x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() �ǵȱ������Σ�
�ǵȱ������Σ�![]() �ڵ�
�ڵ�![]() ����
����![]() ��ֱ��
��ֱ��![]() �ϵĶ��㣬��
�ϵĶ��㣬��![]() �Ƶ�
�Ƶ�![]() ˳ʱ�뷽����ת
˳ʱ�뷽����ת![]() �õ�
�õ�![]() ������
������![]() ��
��![]() ��
��![]() ��
��
��1����ͼ1������![]() ���߶�
���߶�![]() ��ʱ������
��ʱ������![]() ��
��![]() ��������ϵ����ֱ��д�������
��������ϵ����ֱ��д�������
��2����ͼ2������![]() ���߶�
���߶�![]() ���ӳ�����ʱ����1���еĽ��ۻ�����������������֤����Ľ��ۣ�������������д����Ľ��ۣ���֤����Ľ��ۣ�
���ӳ�����ʱ����1���еĽ��ۻ�����������������֤����Ľ��ۣ�������������д����Ľ��ۣ���֤����Ľ��ۣ�
��3����![]() ��ֱ��
��ֱ��![]() ���˶�����
���˶�����![]() �ǵ���ֱ��������ʱ����ֱ��д��
�ǵ���ֱ��������ʱ����ֱ��д��![]() �Ķ�����
�Ķ�����
ͼ1 ͼ2
ͼ2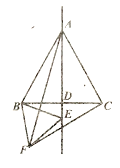 ����ͼ
����ͼ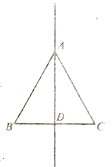
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y��ax2+bx+c��ͼ����ͼ��ʾ���Գ���Ϊֱ��x��1�������н��ۣ�
��abc��0��
������ax2+bx+c��0��������x1����1��x2��3��
��2a+b��0��
��4a2+2b+c��0��
������ȷ���۵����Ϊ_____��
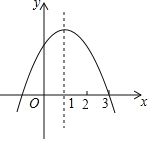
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() ��һ�κ���
��һ�κ���![]() ��ͼ���뷴��������
��ͼ���뷴��������![]() ��ͼ�����������
��ͼ�����������
��1����˷�����������һ�κ����Ľ���ʽ��
��2������ͼ��д��ʹ������������ֵ����һ�κ�����ֵ��xȡֵ��Χ��
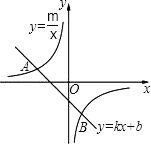
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
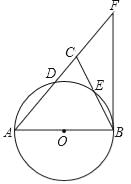
����Ŀ����ͼ������ABC�У�AB��AC����BAC��54������ABΪֱ���ġ�O�ֱ�AC��BC�ڵ�D��E������B��ֱ��BF����AC���ӳ����ڵ�F��
��1����֤��BE��CE��
��2����AB��6����DE�ij���
��3������F�Ķ����Ƕ���ʱ��BF���O���У�֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����108��ƻ���ŵ�һЩ�����У����������ֹ��һ�ֿ���װ10��ƻ����һ�ֿ���װ9��ƻ����һ�ֿ���װ6��ƻ����Ҫ��ÿ�ֹ��Ҫ����ÿ�����Ӿ�ǡ��װ������ͬ��װ������Ϊ_____��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com