
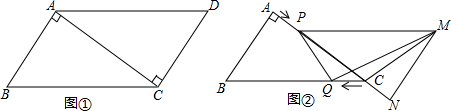
分析 (1)根据勾股定理求得AC的长度,由路程=速度×时间可以得到PC、QC的长度,利用相似三角形的对应边成比例来求P点到BC的距离;
(2)根据勾股定理求出AC,根据PQ∥AB,得出$\frac{CP}{CA}$=$\frac{CQ}{CB}$,$\frac{4-t}{4}$=$\frac{t}{5}$,求解即可;
(3)过点P作PD⊥BC于D,根据△CPD∽△CBA,得出$\frac{4-t}{5}$=$\frac{PD}{3}$,求出PD=$\frac{12}{5}$-$\frac{3}{5}$t,再根据S△QMC=S△QPC,得出y=S△QMC=$\frac{1}{2}$QC•PD,再代入计算即可;
(4)根据PQ⊥MQ得出△PDQ∽△MQP,得出PQ2=MP•DQ,根据勾股定理得出PD2+DQ2=MP•DQ,再分别代入得出($\frac{12-3t}{5}$)2+($\frac{16-9t}{5}$)2=5×$\frac{16-9t}{5}$,求出t即可.
解答 解:(1)依题意得,CQ=t.
∵在Rt△ABC中,AC=$\sqrt{B{C}^{2}-A{B}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴PC=4-t.
设点P到BC的距离为h,则
$\frac{h}{AB}$=$\frac{PC}{BC}$,即$\frac{h}{3}$=$\frac{4-t}{5}$,
解得h=$\frac{12-3t}{5}$.
故答案是:4-t;t;$\frac{12-3t}{5}$.
(2)由平移的性质得MN∥AB,
∵PQ∥MN,
∴PQ∥AB,
∴$\frac{CP}{CA}$=$\frac{CQ}{CB}$,即$\frac{4-t}{4}$=$\frac{t}{5}$,
解得t=$\frac{20}{9}$;
(2)过点P作PD⊥BC于D,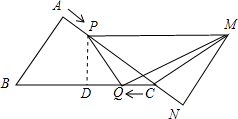
∵△CPD∽△CBA,
∴$\frac{CP}{CB}$=$\frac{PD}{BA}$,
∴$\frac{4-t}{5}$=$\frac{PD}{3}$,
∴PD=$\frac{12}{5}$-$\frac{3}{5}$t,
∵PM∥BC,
∴S△QMC=S△QPC,
∴y=S△QMC=$\frac{1}{2}$QC•PD=$\frac{1}{2}$t($\frac{12}{5}$-$\frac{3}{5}$t)=$\frac{6}{5}$t-$\frac{3}{10}$t2(0<t<4);
(3)若PQ⊥MQ,
则∠PQM=∠PDQ,
∵∠MPQ=∠PQD,
∴△PDQ∽△MQP,
∴$\frac{PQ}{MP}$=$\frac{DQ}{PQ}$,
∴PQ2=MP•DQ,
∴PD2+DQ2=MP•DQ,
∵CD=$\frac{16-4t}{5}$,
∴DQ=CD-CQ=$\frac{16-4t}{5}$-t=$\frac{16-9t}{5}$,
∴($\frac{12-3t}{5}$)2+($\frac{16-9t}{5}$)2=5×$\frac{16-9t}{5}$,
∴t1=0(舍去),t2=$\frac{3}{2}$,
综上所述,当t=$\frac{3}{2}$时,PQ⊥MQ.
点评 此题考查了相似形综合,用到的知识点是相似三角形的判定与性质、勾股定理、平行线的性质、三角形的面积,关键是根据题意画出图形,作出辅助线,构造相似三角形.


科目:初中数学 来源: 题型:解答题
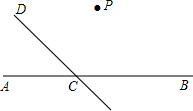 如图,直线CD与直线AB相交于C,根据下列语句画图
如图,直线CD与直线AB相交于C,根据下列语句画图查看答案和解析>>
科目:初中数学 来源: 题型:解答题
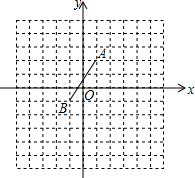 如图,在平面直角坐标系中,已知两点A(1,2),B(-1,-1),
如图,在平面直角坐标系中,已知两点A(1,2),B(-1,-1),查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ($\frac{3}{2}$,0) | B. | (-$\frac{3}{2}$,0) | C. | (0,$\frac{3}{2}$) | D. | ($\frac{2}{3}$,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
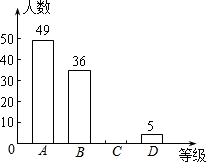 近年来,校园安全问题引起了社会的极大关注,为了让学生了解安全知识,增强安全意识,某校举行了一次“安全知识竞赛”.为了了解这次竞赛的成绩(取整数)情况,从中抽取了部分学生的成绩为一个样本,绘制了如下不完整统计图、表(说明:A级:90分-100分;B级:75分-89分;C级:60分-74分;D级:60分以下).
近年来,校园安全问题引起了社会的极大关注,为了让学生了解安全知识,增强安全意识,某校举行了一次“安全知识竞赛”.为了了解这次竞赛的成绩(取整数)情况,从中抽取了部分学生的成绩为一个样本,绘制了如下不完整统计图、表(说明:A级:90分-100分;B级:75分-89分;C级:60分-74分;D级:60分以下).| 类别 | 频数 (人数) | 频率 |
| A | 49 | 0.49 |
| B | 36 | 0.36 |
| C | m | 0.1 |
| D | 5 | n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com