
【题目】我市为开发沿黄流域小白河渔业资源,鼓励养殖户开展混合养殖,现公布如下政策:![]() 每亩水面年租金为
每亩水面年租金为![]() 元;
元;![]() 每亩水面可在年初混合投放
每亩水面可在年初混合投放![]() 公斤甲种鱼和
公斤甲种鱼和![]() 公斤乙种鱼:经市场调查发现:每公斤甲种鱼的价格为
公斤乙种鱼:经市场调查发现:每公斤甲种鱼的价格为![]() 元,每公斤甲种鱼的饲养费用为
元,每公斤甲种鱼的饲养费用为![]() 元,每公斤甲种鱼当年可获
元,每公斤甲种鱼当年可获![]() 元收益;每公斤乙种鱼的价格为
元收益;每公斤乙种鱼的价格为![]() 元,每公斤乙种鱼的饲养费用为
元,每公斤乙种鱼的饲养费用为![]() 元,每公斤乙种鱼当年可获
元,每公斤乙种鱼当年可获![]() 元收益;
元收益;
(1)某养殖户现有资金![]() 元,他准备再向银行贷款,用于甲乙鱼混合养殖,已知银行贷款的年利率为
元,他准备再向银行贷款,用于甲乙鱼混合养殖,已知银行贷款的年利率为![]() ,试问该养殖户至少应租多少亩水面,并至少向银行贷款多少元,可使年利润不少于
,试问该养殖户至少应租多少亩水面,并至少向银行贷款多少元,可使年利润不少于![]() 元?
元?
(2)为了节省材料该养殖户利用河岸的一角![]() 的两边为边,用总长为
的两边为边,用总长为![]() 米的围网在水库中围成了如图所示的①②③三块区域,其中区域①为直角三角形,区域②③为矩形,而且四边形
米的围网在水库中围成了如图所示的①②③三块区域,其中区域①为直角三角形,区域②③为矩形,而且四边形![]() 为直角梯形.
为直角梯形.
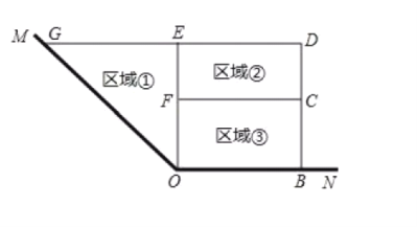
I.若①②③这块区域的面积相等,则![]() 的长为 米;
的长为 米;
II.设![]() 四边形
四边形![]() 的面积为
的面积为![]() 求
求![]() 与
与![]() 之的函数关系式,并说明
之的函数关系式,并说明![]() 为何值时,
为何值时,![]() 有最大值?最大值是多少?
有最大值?最大值是多少?
【答案】(1)该养殖户至少应租![]() 亩水面,至少向银行贷款
亩水面,至少向银行贷款![]() 元;(2)I
元;(2)I![]() ;II当
;II当![]() 时,
时,![]() 有最大值,最大值为
有最大值,最大值为![]() .
.
【解析】
(1)首先根据题目计算得出混合养殖的利润(每亩的年利润),再设应该租x亩水面,根据年利润减去银行贷款利息大于等于36600列出不等式求解即可;
(2)I.利用一元二次方程求解即可;II.由已知得出![]() ,继而得出
,继而得出![]() ,可得出四边形
,可得出四边形![]() 的面积为
的面积为![]() ,化为顶点式,即可得出答案.
,化为顶点式,即可得出答案.
解:![]() 苗种费用
苗种费用![]() (元)
(元)
饲养费![]() (元)
(元)
成本![]() (元)
(元)
收益![]() (元)
(元)
利润(每亩的年利润)![]() (元)
(元)
![]() 设该养殖户应租
设该养殖户应租![]() 亩水面.
亩水面.
根据题意列出不等式:![]() ,
,
解得:![]() .
.
则该养殖户至少应租![]() 亩水面,至少向银行贷款
亩水面,至少向银行贷款![]() 元
元
答:该养殖户至少应租![]() 亩水面,至少向银行贷款
亩水面,至少向银行贷款![]() 元.
元.
![]() 由题意可知,
由题意可知,![]()
![]() ,
,![]() ,
,
设![]()
则![]()
I.![]() 这块区域的面积相等,
这块区域的面积相等,
![]()
![]() 或
或![]() (舍弃),
(舍弃),
![]() .
.
答:当![]() 这块区域的面积相等时
这块区域的面积相等时![]() 长
长![]() 米.
米.
II. 由题意可知,![]() ,
,![]() ,
,
![]()
![]() ,
,
则![]()
四边形![]() 的面积为
的面积为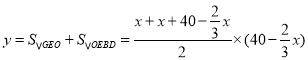 ,
,
整理得![]()
![]()
且![]()
![]() 当
当![]() 时,
时,![]() 有最大值,最大值为
有最大值,最大值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在甲、乙两个不透明的布袋里,都装有3个大小、材质完全相同的小球,其中甲袋中的小球上分别标有数字0,1,2;乙袋中的小球上分别标有数字﹣1,﹣2,0.现从甲袋中任意摸出一个小球,记其标有的数字为x,再从乙袋中任意摸出一个小球,记其标有的数字为y,以此确定点M的坐标(x,y).
(1)请你用画树状图或列表的方法,写出点M所有可能的坐标;
(2)求点M(x,y)在函数y=﹣![]() 的图象上的概率.
的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线相交于O,E是OD的中点,DF∥AC交CE延长线于点F,连接AF.
(1)求证:四边形AODF是菱形.
(2)若∠AFC=90°,AB=2,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于
轴交于![]() ,其中
,其中![]() ,点
,点![]() 为抛物线上一动点,过点
为抛物线上一动点,过点![]() 作
作![]() 平行
平行![]() 交抛物线于
交抛物线于![]() ,
,
(1)求抛物线的解析式;
(2)①当![]() 两点重合时时,
两点重合时时,![]() 所在直线解析式为_____________.
所在直线解析式为_____________.
②在①的条件下,取线段![]() 中点
中点![]() ,连接
,连接![]() ,判断以点
,判断以点![]() 为顶点的四边形是什么四边形,并说明理由?
为顶点的四边形是什么四边形,并说明理由?
(3)已知 ,连接
,连接![]() ,
,![]() 轴,交
轴,交![]() 于
于![]() ,
,![]() 轴上有一动点
轴上有一动点![]() ,
,![]() ,
,![]() 的长为______.
的长为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=x2﹣4x+n(x>0)的图象记为G1,将G1绕坐标原点旋转180°得到图象G2,图象G1和G2合起来记为图象G.
(1)若点P(﹣1,2)在图象G上,求n的值.
(2)当n=﹣1时.
①若Q(t,1)在图象G上,求t的值.
②当k≤x≤3(k<3)时,图象G对应函数的最大值为5,最小值为﹣5,直接写出k的取值范围.
(3)当以A(﹣3,3)、B(﹣3,﹣1)、C(2,﹣1)、D(2,3)为顶点的矩形ABCD的边与图象G有且只有三个公共点时,直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,∠ACB=90°,BC=3,AC=4,小红按如下步骤作图:
①分别以A、C为圆心,以大于![]() AC的长为半径在AC两边作弧,交于两点M、N;
AC的长为半径在AC两边作弧,交于两点M、N;
②连接MN,分别交AB、AC于点D、O;
③过C作CE∥AB交MN于点E,连接AE、CD.
则四边形ADCE的周长为( )

A. 10 B. 20 C. 12 D. 24
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com