
【题目】幻方的历史很悠久,传统幻方最早出现在夏禹时代的“洛书”,“洛书”用今天的数学符号翻译出来,就是一个三阶幻方,如图1所示,图中每个位置上的点数就表示数几,如中间5个点就表示5,每横行、每竖列以及两条对角线上的数的和都相等.
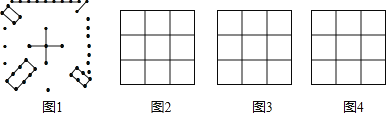
(1)把﹣4,﹣3,﹣2,﹣1,0,1,2,3,4填入如图2的方格中,使每横行、每竖列以及两条对角线上的数的和都相等;
(2)若把3x﹣8,3x﹣6,3x﹣4,3x﹣2,3x,3x+2,3x+4,3x+6,3x+8填入如图3的方格中,使每横行、每竖列以及两条对角线上的数的和都相等,则每行的和是 (用含x的式子表示);
(3)根据上述填数经验请把﹣2,﹣22,﹣23,﹣24,﹣25,﹣26,﹣27,﹣28,﹣29填入如图4的方格中,使每横行、每竖列以及两条对角线上的数的积都相等.
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(10,0),(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国是水资源比较贫乏的国家之一,为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段来达到节约用水的目的,规定如下用水收费标准:每户每月的用水不超过20立方米(含20立方米)时,水费按“基本价”收费:超过20立方米时,不超过的部分仍按“基本价”收费,超过部分按“调节价”收费.某户居民今年4、5月份的用水量和水费如下表所示:
月份 | 用水量(立方米) | 水费(元) |
4 | 20 | 42 |
5 | 24 | 56.40 |
(1)请你算一算该市水费的“调节价”每立方米多少元?
(2)若该户居民6月份用水量为30立方米,请算一算,6月份水费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,一次函数y=﹣2x+8的图象与x轴,y轴分别交于点A,点C,过点A作AB⊥x轴,垂足为点A,过点C作CB⊥y轴,垂足为点C,两条垂线相交于点B.

(1)线段AB,BC,AC的长分别为AB= ,BC= ,AC= ;
(2)折叠图1中的△ABC,使点A与点C重合,再将折叠后的图形展开,折痕DE交AB于点D,交AC于点E,连接CD,如图2.
请从下列A、B两题中任选一题作答,我选择 题.
A:①求线段AD的长;
②在y轴上,是否存在点P,使得△APD为等腰三角形?若存在,请直接写出符合条件的所有点P的坐标;若不存在,请说明理由.
B:①求线段DE的长;
②在坐标平面内,是否存在点P(除点B外),使得以点A,P,C为顶点的三角形与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车从仓库O出发在东西街道上运送水果,规定向东为正方向,一次到达的5个销售地点分别为A,B,C,D,E,最后回到仓库O,货车行驶的记录(单位:千米)如下:+2,+3,﹣6,﹣1,﹣2,+4.请问:
(1)请以仓库O为原点,向东为正方向,选择适当的单位长度,画出数轴,并标出A,B,C,D,E的位置;
(2)试求出该货车共行驶了多少千米?
(3)如果货车运送的水果以100千克为标准重量,超过的千克数记为正数,不足的千克数记为负数,则运往A,B,C,D,E五个地点的水果重量可记为:+50,﹣15,+25,﹣10,﹣20,则该货车运送的水果总重量是多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗,某食品厂为了解市民对去年销售量较好的肉馅粽、豆沙粽、红枣粽、蛋黄馅粽(以下分别用A,B,C,D表示这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查结果绘制成如下两幅统计图.
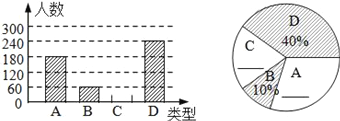
请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?将不完整的条形图和扇形图补充完整;
(2)若居民区有8000人,请估计爱吃C ,D粽的总人数;
(3)若有外型完全相同的A,B,C,D粽各一个煮熟后,小王吃了两个,用列表或画树状图的方法,求他第二个吃到的恰好是C粽的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司经营杨梅业务,以3万元/吨的价格买入杨梅后,分拣成A、B两类,A类杨梅包装后直接销售,包装成本为1万元/吨,它的平均销售价格y(单位:万元/吨)与销售数量x(![]() ≥2,单位:吨)之间的函数关系如图所示;B类杨梅深加工后再销售,深加工总费用s(单位:万元)与加工数量t(单位:吨)之间的函数关系是
≥2,单位:吨)之间的函数关系如图所示;B类杨梅深加工后再销售,深加工总费用s(单位:万元)与加工数量t(单位:吨)之间的函数关系是![]() ,平均销售价格为9万元/吨.
,平均销售价格为9万元/吨.
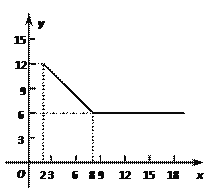
(1)A类杨梅的销售量为5吨时,它的平均销售价格是每吨多少万元?
(2)若该公司收购10吨杨梅,其中A类杨梅有4吨,则经营这批杨梅所获得的毛利润(w)为多少万元?(毛利润=销售总收入-经营总成本)
(3)若该公司收购20吨杨梅,其中A类杨梅有x吨,经营这批杨梅所获得的毛利润为w万元.
①求w关于x的函数关系式;
②若该公司获得了30万元毛利润,问:用于直销的A类杨梅有多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
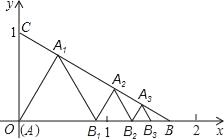
【题目】如图所示,已知直线![]() 与x、y轴交于B、C两点,A(0,0),在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…则第n个等边三角形的边长等于( )
与x、y轴交于B、C两点,A(0,0),在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…则第n个等边三角形的边长等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
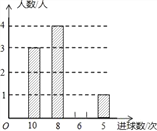
【题目】某校九年级学生在一节体育课中,选一组学生进行投篮比赛,每人投10次,汇总投进球数的情况进行统计分析,绘制了如下不完整的统计表和统计图.
次数 | 10 | 8 | 6 | 5 |
人数 | 3 | a | 2 | 1 |
(1)表中a= ;
(2)请将条形统计图补充完整;
(3)从小组成员中选一名学生参加校动会投篮比赛,投进10球的成员被选中的概率为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com