
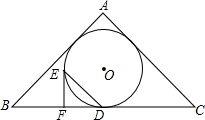
 如图,在△ABC中,AB=AC=5,BC=7,△ABC的内切圆⊙O与边BC相切于点D,过点D作DE∥AC交⊙O于点E,过点E作⊙O的切线交BC于点F,则DE-EF的值等于( )
如图,在△ABC中,AB=AC=5,BC=7,△ABC的内切圆⊙O与边BC相切于点D,过点D作DE∥AC交⊙O于点E,过点E作⊙O的切线交BC于点F,则DE-EF的值等于( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{4}$ |
分析 首先根据等腰三角形的性质得出BD=DC,以及利用平行线的性质得出GD=2.5,再利用切割线定理求出EF的长,再利用△ABC∽△DEF,得出$\frac{FD}{EF}$=$\frac{AB}{BC}$,即可得求出PM的长,进而得出DE-EF的值.
解答 解:∵AB=AC=5,BC=7,△ABC的内切圆⊙O与边BC相切于点D(利用等腰三角形三线合一,)
∴BD=CD=3.5,
延长DE交AB于点G,
∵DE∥AC,
∴∠C=∠EDF,GD=$\frac{1}{2}$BC=2.5,
∴AG=BG=2.5,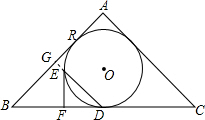
设⊙O与边AB相切于点R,
则BR=BD=3.5,
∴GR=3.5-2.5=1,
∵GR 2=GE×GD,
∴1=GE×2.5,
解得:GE=0.4,
∴DE=GD-GE=2.5-0.4=2.1,
∵∠C=∠EDF,FE=FD(切线长定理),
∴∠FED=∠FDE=∠C=∠B,
∴△ABC∽△DEF,
∴$\frac{FD}{ED}=\frac{AB}{BC}$,
即$\frac{FD}{2.1}$=$\frac{5}{7}$,
解得:DF=1.5,
∴EF=1.5,则
∴DE-EF=2.1-1.5=0.6.
故选:C.
点评 此题主要考查了三角形内切圆的性质以及切线长定理和相似三角形的判定等性质,得出MN的长度和△ABC∽△DEF是解决问题的关键.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
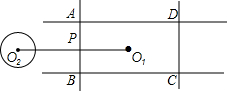 如图,矩形ABCD的长为20,宽为14,点O1为矩形的中心,⊙O2的半径为5,O1O2⊥AB于点P,O1O2=23.若⊙O2绕点P按顺时针方向旋转360°,在旋转过程中,⊙O2与矩形的边所在的直线相切的位置一共出现( )
如图,矩形ABCD的长为20,宽为14,点O1为矩形的中心,⊙O2的半径为5,O1O2⊥AB于点P,O1O2=23.若⊙O2绕点P按顺时针方向旋转360°,在旋转过程中,⊙O2与矩形的边所在的直线相切的位置一共出现( )| A. | 18次 | B. | 12次 | C. | 8次 | D. | 4次 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
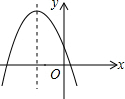 抛物线y=ax2+bx+c(a≠0)大致图象如图所示,则双曲线y=$\frac{b}{ax}$图象在( )
抛物线y=ax2+bx+c(a≠0)大致图象如图所示,则双曲线y=$\frac{b}{ax}$图象在( )| A. | 一、三象限 | B. | 一、二象限 | C. | 二、三象限 | D. | 二、四象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
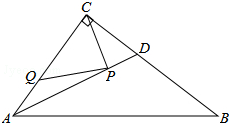 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是$\frac{24}{5}$.
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是$\frac{24}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
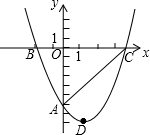 如图,经过点A(0,-6)的抛物线y=$\frac{1}{2}$x2+bx+c与x轴相交于B(-2,0),C两点.
如图,经过点A(0,-6)的抛物线y=$\frac{1}{2}$x2+bx+c与x轴相交于B(-2,0),C两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com