
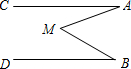
 如图,AC∥DB,∠A=20°,∠B=30°,那么∠AMB=50°.
如图,AC∥DB,∠A=20°,∠B=30°,那么∠AMB=50°. 科目:初中数学 来源: 题型:解答题
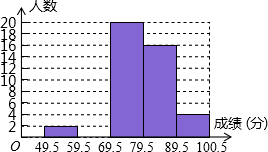 某班数学科代表小红对本班上学期期末考试成绩作了统计分析,绘制成如下频数,频率统计表和频率分布直方图.请你根据图表中提供的信息解答下列问题,
某班数学科代表小红对本班上学期期末考试成绩作了统计分析,绘制成如下频数,频率统计表和频率分布直方图.请你根据图表中提供的信息解答下列问题,| 分组 | 49.5-59.5 | 59.5-69.5 | 69.5-79.5 | 79.5-89.5 | 89.5-100.5 | 合计 |
| 频数 | 2 | a | 20 | 16 | 4 | 50 |
| 频率 | 0.04 | 0.16 | 0.4 | 0.32 | b | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
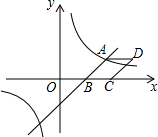 如图,已知一次函数y=$\frac{3}{2}$x-3与反比例函数y=$\frac{k}{x}$的图象相交于点A(4,n),与x轴相交于点B.
如图,已知一次函数y=$\frac{3}{2}$x-3与反比例函数y=$\frac{k}{x}$的图象相交于点A(4,n),与x轴相交于点B.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a+b)2=a2-2ab+b2 | B. | (a-b)2=a2-b2 | C. | (a+b)(-a+b)=b2-a2 | D. | (a+b)(-a-b)=a2-b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知长方形ABCD,AB=CD=4,BC=AD=6,∠A=∠B=∠C=∠D=90°,E为CD边的中点,P为长方形ABCD边上的动点,动点P从A出发,沿着A→B→C→E运动到E点停止,设点P经过的路程为x,△APE的面积为y.
如图,已知长方形ABCD,AB=CD=4,BC=AD=6,∠A=∠B=∠C=∠D=90°,E为CD边的中点,P为长方形ABCD边上的动点,动点P从A出发,沿着A→B→C→E运动到E点停止,设点P经过的路程为x,△APE的面积为y.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
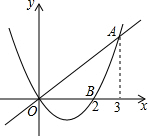 如图,已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A(3,2),与x轴交于点B(2,0),若0<y1<y2,则x的取值范围是( )
如图,已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A(3,2),与x轴交于点B(2,0),若0<y1<y2,则x的取值范围是( )| A. | 0<x<2 | B. | 0<x<3 | C. | 2<x<3 | D. | x<0或x>3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
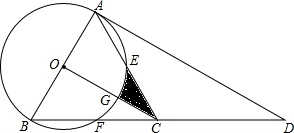 如图,点D是等边△ABC中BC边的延长线上一点,且AC=CD,以AB为直径作⊙O,分别交边AC、BC于点E、点F
如图,点D是等边△ABC中BC边的延长线上一点,且AC=CD,以AB为直径作⊙O,分别交边AC、BC于点E、点F查看答案和解析>>
科目:初中数学 来源: 题型:选择题
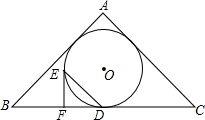 如图,在△ABC中,AB=AC=5,BC=7,△ABC的内切圆⊙O与边BC相切于点D,过点D作DE∥AC交⊙O于点E,过点E作⊙O的切线交BC于点F,则DE-EF的值等于( )
如图,在△ABC中,AB=AC=5,BC=7,△ABC的内切圆⊙O与边BC相切于点D,过点D作DE∥AC交⊙O于点E,过点E作⊙O的切线交BC于点F,则DE-EF的值等于( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com