
【题目】如图,将边长为8的等边![]() 置于平面直角坐标系中,点
置于平面直角坐标系中,点![]() 在
在![]() 轴正半轴上,过点
轴正半轴上,过点![]() 作
作![]() 于点
于点![]() ,将
,将![]() 绕着原点
绕着原点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,这时,点
,这时,点![]() 恰好落在
恰好落在![]() 轴上.若动点
轴上.若动点![]() 从原点
从原点![]() 出发,沿线段
出发,沿线段![]() 向终点
向终点![]() 运动,动点
运动,动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 向终点
向终点![]() 运动,两点同时出发,速度均为每秒1个单位长度.设运动的时间为
运动,两点同时出发,速度均为每秒1个单位长度.设运动的时间为![]() 秒.
秒.
(1)请直接写出点![]() 、点
、点![]() 的坐标;
的坐标;
(2)当![]() 的面积为
的面积为![]() 时,求
时,求![]() 的值;
的值;
(3)设![]() 与
与![]() 相交于点
相交于点![]() ,当
,当![]() 为何值时,
为何值时, ![]() 与
与![]() 相似?
相似?

【答案】(1)![]() ,
, ![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 秒或
秒或![]() 秒时,
秒时, ![]() 与
与![]() 相似.
相似.
【解析】试题分析:(1)根据等边三角形的性质可直接得出A点坐标;再由OC⊥AB可得出OC的长,根据图形旋转不变性的性质可得出OD的长,进而得出D点坐标;
(2)过点E作EG⊥OD于点G,根据等边三角形的性质可知OC平分∠AOB,再根据锐角三角函数的定义求出EG的长,S△OEF=![]() OFEG,OF=OD﹣DF=
OFEG,OF=OD﹣DF=![]() ﹣t即可得出t的值;
﹣t即可得出t的值;
(3)由于∠BOD=∠FOP,△OPF∽△ODB和△OPF∽△OBD两种情况进行讨论.
试题解析:解:(1)∵等边△AOB的边长为8,点A在x轴正半轴上,∴A(8,0),∵OC⊥AB,∴∠AOC=30°,∴OC=OAcos30°=8×![]() =
=![]() ,∵△OAC旋转后OC与OD重合,∴D(0,
,∵△OAC旋转后OC与OD重合,∴D(0, ![]() );
);
(2)过点E作EG⊥OD于点G,如图①所示:
∵△OAB为等边三角形,OC⊥AB,∴OC平分∠AOB,∴∠AOC=30°,∴∠EOG=90°﹣30°=60°,∴EG=OEsin∠EOG=![]() t,又∵S△OEF=
t,又∵S△OEF=![]() OFEG,OF=OD﹣DF=
OFEG,OF=OD﹣DF=![]() ﹣t,由题意可得:
﹣t,由题意可得: ![]() (
(![]() ﹣t)
﹣t)![]() t=
t=![]() ,解得t=
,解得t=![]() ±3;
±3;
(3)因为∠BOD=∠FOP,所以应分两种情况讨论:
①当∠FPO=∠BDO=90°时,如图②,∵△OPF∽△ODB,此时OE=OF,∴t=![]() ﹣t,解得:t=
﹣t,解得:t=![]() ;
;
②当∠OFP=∠ODB=90°时,如图③,∵△OPF∽△OBD,∴OF=![]() OE,即(
OE,即(![]() ﹣t)=
﹣t)=![]() t,解得:t=
t,解得:t=![]() .
.
综上所述,当t=![]() 秒或t=
秒或t=![]() 秒时,△OPF与△OBD相似.
秒时,△OPF与△OBD相似.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1+∠2=180o, ∠3=∠B,试说明∠DEC+∠C=180o.请完成下列填空:

解:∵∠1+∠2=180o(已知)
又∵∠1+∠4=180o(平角定义)
∴∠2=∠4(________)
∴______∥______(_________)
∴∠3 = ∠ADE(__________)
又∵∠3=∠B(已知)
∴∠ADE=∠B(等量代换)
∴BC∥_____(_________)
∴∠DEC+∠C=180o(__________)
查看答案和解析>>
科目:初中数学 来源: 题型:
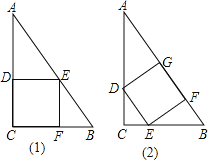
【题目】直角三角形的铁片ABC的两条直角边BC,AC的长分别为3cm和4cm,如图所示分别采用⑴,⑵两种方法,剪去一块正方形铁片,为了使剪去正方形铁片后剩下的边角料较少,试比较哪一种剪法较为合理,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明将连续的奇数1,3,5,7,9,…,排成如图所示的数阵,用一个矩形框框住其中的9个数,如图所示.
(1)矩形阴影框中的9个数的和与中间一个数存在怎样的关系?(直接写出笞案)
(2)若将矩形框上下左右移动,这个关系还成立吗?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示数表是由从1 开始的连续自然数组成,观察规律并完成各题的解答.
(1)表中第3行共有_________个数,第3行各数之和是_________;
(2)表中第8行的最后一个数是_________,第8行共有_________个数;
(3)用含n的代数式表示:第n行的第一个数是_________,最后一个数是_________,第n行共有_________个数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】淇淇和嘉嘉在学习了利用相似三角形测高之后分别测量两个旗杆高度.
(1)如图1所示,淇淇将镜子放在地面上,然后后退直到她站直身子刚好能从镜子里看到旗杆的顶端E,测得脚掌中心位置B到镜面中心C的距离是50cm,镜面中心C距离旗杆底部D的距离为4m,已知淇淇同学的身高是1.54m,眼睛位置A距离淇淇头顶的距离是4cm,求旗杆DE 的高度.

如图2所示,嘉嘉在某一时刻测得 1 米长的竹竿竖直放置时影长2米,在同时刻测量旗杆的影长时,旗杆的影子一部分落在地面上(BC),另一部分落在斜坡上(CD),他测得落在地面上的影长为10米,落在斜坡上的影长为![]() 米,∠DCE=45°,求旗杆AB的高度?
米,∠DCE=45°,求旗杆AB的高度?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
如图1,![]() 和
和![]() 都是等腰直角三角形,其中
都是等腰直角三角形,其中![]() ,点
,点![]() 在线段
在线段![]() 上.
上.

操作发现:如图2,保持点![]() 不动,
不动,![]() 绕点
绕点![]() 按顺时针旋转角度
按顺时针旋转角度![]() (
(![]() ),连接
),连接![]() 与
与![]() .
.

(1)猜想线段![]() ,
,![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
拓展探究:如图3,![]() 绕点
绕点![]() 继续按顺时针旋转,当点
继续按顺时针旋转,当点![]() ,
,![]() ,
,![]() 在同一直线上时,过点
在同一直线上时,过点![]() 作
作![]() ,垂足为
,垂足为![]() .
.

(2)求![]() 的度数;
的度数;
(3)直接写出线段![]() ,
,![]() ,
,![]() 之间的的数量关系.
之间的的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com