
 如图,在矩形纸片ABCD中,AB=6,BC=8.把△BCD沿对角线BD折叠,使点C落在C′处,BC′交AD于点G;E、F分别是C′D和BD上的点,线段EF交AD于点H,把△FDE沿EF折叠,使点D落在D′处,点D′恰好与点A重合.
如图,在矩形纸片ABCD中,AB=6,BC=8.把△BCD沿对角线BD折叠,使点C落在C′处,BC′交AD于点G;E、F分别是C′D和BD上的点,线段EF交AD于点H,把△FDE沿EF折叠,使点D落在D′处,点D′恰好与点A重合.| AG |
| BG |
| AG |
| BG |
| 1 |
| 2 |
|
| 7 |
| 4 |
| AG |
| BG |
| ||
|
| 7 |
| 25 |
| 1 |
| 2 |
| 7 |
| 24 |
| 7 |
| 24 |
| 7 |
| 24 |
| 7 |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 6 |
| 25 |
| 6 |


科目:初中数学 来源: 题型:
 某文具零售店老板到批发市场选购A、B两种文具,批发价分别为12元/件,8元/件,若该店零售的A、B两种文具的日销售y(件)与零售价x(元/件)均成一次函数图象如图所示.
某文具零售店老板到批发市场选购A、B两种文具,批发价分别为12元/件,8元/件,若该店零售的A、B两种文具的日销售y(件)与零售价x(元/件)均成一次函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:
| A、-6x2-8y2-4 |
| B、10x2-8y2-4 |
| C、-6x2-8y2+4 |
| D、10x2-8y2+4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,四边形ABCD是边长为6的正方形,P是BC的中点,过点P作直线交AD于点E,交AB延长线于点F,设AE=x.
如图,四边形ABCD是边长为6的正方形,P是BC的中点,过点P作直线交AD于点E,交AB延长线于点F,设AE=x.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
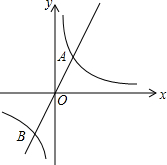 阅读理解并填空:
阅读理解并填空:| 1 |
| x+2 |
| 1 |
| x |
| 1 |
| x |
| 6 |
| x |
| 6 |
| x |
| 3 |
| 2 |
| 6 |
| x |
| 6 |
| x-n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com