
 如图,△ABC和△DEF分别是⊙O的外切正三角形和内接正三角形,则它们的面积比为( )
如图,△ABC和△DEF分别是⊙O的外切正三角形和内接正三角形,则它们的面积比为( )| A、4 | ||
| B、2 | ||
C、
| ||
D、
|
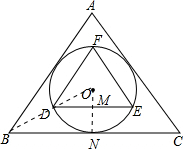 解:过点O作ON⊥BC垂足为N,交DE于点M,连接OB,则O,D,B三点一定共线,
解:过点O作ON⊥BC垂足为N,交DE于点M,连接OB,则O,D,B三点一定共线,| 3 |
| 3 |
| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| S△ABC |
| S△DEF |
12
| ||
3
|


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
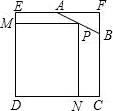 如图,已知边长为4的正方形截取一个角后成为五边形ABCDE,其中AF=2,BF=1.P是AB边上的任一点,过P作PN⊥DC于N,PM⊥DE于M,设PN=x,矩形PNDM的面积为y,当x为何值时,矩形PNDM的面积最大,并求出最大面积.
如图,已知边长为4的正方形截取一个角后成为五边形ABCDE,其中AF=2,BF=1.P是AB边上的任一点,过P作PN⊥DC于N,PM⊥DE于M,设PN=x,矩形PNDM的面积为y,当x为何值时,矩形PNDM的面积最大,并求出最大面积.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在矩形纸片ABCD中,AB=6,BC=8.把△BCD沿对角线BD折叠,使点C落在C′处,BC′交AD于点G;E、F分别是C′D和BD上的点,线段EF交AD于点H,把△FDE沿EF折叠,使点D落在D′处,点D′恰好与点A重合.
如图,在矩形纸片ABCD中,AB=6,BC=8.把△BCD沿对角线BD折叠,使点C落在C′处,BC′交AD于点G;E、F分别是C′D和BD上的点,线段EF交AD于点H,把△FDE沿EF折叠,使点D落在D′处,点D′恰好与点A重合.| AG |
| BG |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,△ABC和△ADE均是顶角为42°的等腰三角形,BC、DE分别是底边,图中的△ABD绕A旋转42°后得到的图形是
如图,△ABC和△ADE均是顶角为42°的等腰三角形,BC、DE分别是底边,图中的△ABD绕A旋转42°后得到的图形是查看答案和解析>>
科目:初中数学 来源: 题型:
 数学在我们的生活中无处不在,就连小小的台球桌上都有数学问题.如图所示,∠1=∠2,若∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证∠1等于
数学在我们的生活中无处不在,就连小小的台球桌上都有数学问题.如图所示,∠1=∠2,若∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证∠1等于查看答案和解析>>
科目:初中数学 来源: 题型:
| A、4cm | B、5cm |
| C、6cm | D、7cm |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,点P、Q分别为矩形ABCD中AB、BC上两点,AB=18cm、AD=4cm,AP=2x,BQ=x,设△PBQ的面积为y(cm2).
如图,点P、Q分别为矩形ABCD中AB、BC上两点,AB=18cm、AD=4cm,AP=2x,BQ=x,设△PBQ的面积为y(cm2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com