
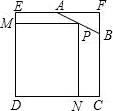
 如图,已知边长为4的正方形截取一个角后成为五边形ABCDE,其中AF=2,BF=1.P是AB边上的任一点,过P作PN⊥DC于N,PM⊥DE于M,设PN=x,矩形PNDM的面积为y,当x为何值时,矩形PNDM的面积最大,并求出最大面积.
如图,已知边长为4的正方形截取一个角后成为五边形ABCDE,其中AF=2,BF=1.P是AB边上的任一点,过P作PN⊥DC于N,PM⊥DE于M,设PN=x,矩形PNDM的面积为y,当x为何值时,矩形PNDM的面积最大,并求出最大面积. 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 如图,有背面一样,正面分别是2、3、4、5的4张扑克牌,两次随机摸一张牌看正面的点数(每一次摸牌后放回)
如图,有背面一样,正面分别是2、3、4、5的4张扑克牌,两次随机摸一张牌看正面的点数(每一次摸牌后放回)查看答案和解析>>
科目:初中数学 来源: 题型:
 某文具零售店老板到批发市场选购A、B两种文具,批发价分别为12元/件,8元/件,若该店零售的A、B两种文具的日销售y(件)与零售价x(元/件)均成一次函数图象如图所示.
某文具零售店老板到批发市场选购A、B两种文具,批发价分别为12元/件,8元/件,若该店零售的A、B两种文具的日销售y(件)与零售价x(元/件)均成一次函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:
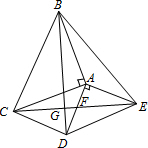 如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连结CE交AD于点F,连接BD交CE于点G,则tan∠FDG=
如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连结CE交AD于点F,连接BD交CE于点G,则tan∠FDG=查看答案和解析>>
科目:初中数学 来源: 题型:
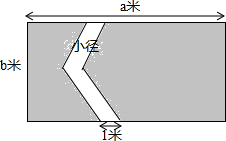 如图,某公园中有一块长a米,宽b米的长方形草坪,为方便游客穿行同时也避免草坪被随意践踏,草坪上用石子铺设了一条宽度均为1米的小径,求铺设小径后草坪(阴影部分)的面积.
如图,某公园中有一块长a米,宽b米的长方形草坪,为方便游客穿行同时也避免草坪被随意践踏,草坪上用石子铺设了一条宽度均为1米的小径,求铺设小径后草坪(阴影部分)的面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com