
 如图,四边形ABCD是边长为6的正方形,P是BC的中点,过点P作直线交AD于点E,交AB延长线于点F,设AE=x.
如图,四边形ABCD是边长为6的正方形,P是BC的中点,过点P作直线交AD于点E,交AB延长线于点F,设AE=x.| EM |
| BF |
| MP |
| BP |
| 18 |
| x-3 |
 解:(1)如图,过点E作EM∥AP;
解:(1)如图,过点E作EM∥AP;| EM |
| BF |
| MP |
| BP |
| 18 |
| x-3 |
| 18 |
| x-3 |


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
 如图,在矩形纸片ABCD中,AB=6,BC=8.把△BCD沿对角线BD折叠,使点C落在C′处,BC′交AD于点G;E、F分别是C′D和BD上的点,线段EF交AD于点H,把△FDE沿EF折叠,使点D落在D′处,点D′恰好与点A重合.
如图,在矩形纸片ABCD中,AB=6,BC=8.把△BCD沿对角线BD折叠,使点C落在C′处,BC′交AD于点G;E、F分别是C′D和BD上的点,线段EF交AD于点H,把△FDE沿EF折叠,使点D落在D′处,点D′恰好与点A重合.| AG |
| BG |
查看答案和解析>>
科目:初中数学 来源: 题型:
 数学在我们的生活中无处不在,就连小小的台球桌上都有数学问题.如图所示,∠1=∠2,若∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证∠1等于
数学在我们的生活中无处不在,就连小小的台球桌上都有数学问题.如图所示,∠1=∠2,若∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证∠1等于查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
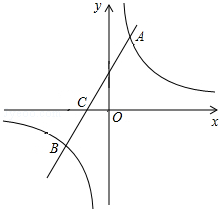 如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=
如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=| m |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com