Question

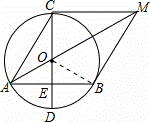
如图，已知AB是⊙O的弦，CD是⊙O的直径，CD⊥AB，垂足为E，且点E是OD的中点，⊙O的切线BM与AO的延长线相交于点M，连接AC，CM．

（1）若AB=4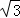，求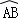的长；（结果保留π）

（2）求证：四边形ABMC是菱形．

Answer 1

（1）解：∵OA=OB，E为AB的中点，

∴∠AOE=∠BOE，OE⊥AB，

∵OE⊥AB，E为OD中点，

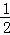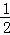∴OE=OD=OA，

∴在Rt△AOE中，∠OAB=30°，∠AOE=60°，∠AOB=120°，

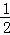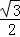设OA=x，则OE=x，AE=x，

∵AB=4，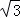

∴AB=2AE=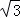x=4，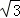

解得：x=4，

则的长l==；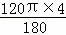

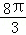（2）证明：由（1）得∠OAB=∠OBA=30°，∠BOM=∠COM=60°，∠AMB=30°，

∴∠BAM=∠BMA=30°，

∴AB=BM，

∵BM为圆O的切线，

∴OB⊥BM，

在△COM和△BOM中，

，

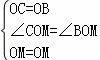∴△COM≌△BOM（SAS），

∴CM=BM，∠CMO=∠BMO=30°，

∴CM=AB，∠CMO=∠MAB，

∴CM∥AB，

∴四边形ABMC为菱形．