
【题目】一副三角板的两个直角重叠在一起,∠A=30°,∠C=45°,△COD固定不动,△AOB绕着O点逆时针旋转α°(0°<α<180° ),使两个三角形至少有一组边所在直线垂直,则α=_____.

【答案】45°或60°或90°或105°或135°或150°.
【解析】
将△AOB绕点O逆时针旋转α度(0°<α<180°),分别根据BO⊥CD,AB⊥OD,AO⊥DO,AB⊥CD,AO⊥CD,AB⊥CO,即可得出α为45°或60°或90°或105°或135°或150°.
如图所示,①当α为45°时,BO⊥CD;

②当α为60°时,AB⊥OD;
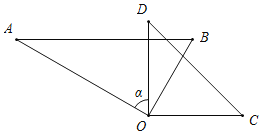
③当α为90°时,AO⊥DO;
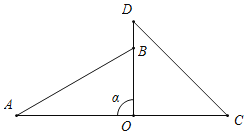
④当α为105°时,AB⊥CD;

⑤当α为135°时,AO⊥CD;
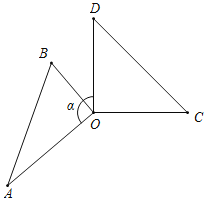
⑥当α为150°时,AB⊥CO.
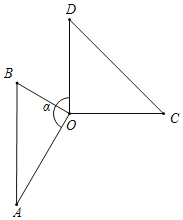
综上所述,将△AOB绕点O逆时针旋转α度(0°<α<180°),当α为45°或60°或90°或105°或135°或150°时,两个三角形至少有一组边所在直线垂直
故答案为:45°或60°或90°或105°或135°或150°


科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB内任意一点,且∠AOB=40°,点M和点N分别是射线OA和射线OB上的动点,当△PMN周长取最小值时,则∠MPN的度数为( )

A. 140° B. 100° C. 50° D. 40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAC中,以O为圆心,OA为半径作⊙O,作OB⊥OC交⊙O于B,垂足为O,连接AB交OC于点D,∠CAD=∠CDA.
(1)判断AC与⊙O的位置关系,并证明你的结论;
(2)若OA=5,OD=1,求线段AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂修建了甲、乙两个水池,最大蓄水量都是1200立方米,如果甲池有水480立方米,乙池蓄满水,甲池每小时进水80立方米,乙池每小时放水100立方米.
(1)分别写出甲、乙两池的水量![]() 与时间
与时间![]() 的函数解析式;
的函数解析式;
(2)甲、乙两池同时进水、放水,经过几小时两个水池内的水一样多?
查看答案和解析>>
科目:初中数学 来源: 题型:
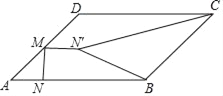
【题目】如图,在平行四边形ABCD中,∠A=45°,AB=4,AD=2![]() ,M是AD边的中点,N是AB边上一动点,将线段M绕点M逆时针旋转90至MN′,连接N′B,N′C,则N′B+N′C的最小值是_____.
,M是AD边的中点,N是AB边上一动点,将线段M绕点M逆时针旋转90至MN′,连接N′B,N′C,则N′B+N′C的最小值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究:
(1)如图①所示是一个半径为![]() ,高为4的圆柱体和它的侧面展开图,AB是圆柱的一条母线,一只蚂蚁从A点出发沿圆柱的侧面爬行一周到达B点,求蚂蚁爬行的最短路程.(探究思路:将圆柱的侧面沿母线AB剪开,它的侧面展开图如图①中的矩形
,高为4的圆柱体和它的侧面展开图,AB是圆柱的一条母线,一只蚂蚁从A点出发沿圆柱的侧面爬行一周到达B点,求蚂蚁爬行的最短路程.(探究思路:将圆柱的侧面沿母线AB剪开,它的侧面展开图如图①中的矩形![]() 则蚂蚁爬行的最短路程即为线段
则蚂蚁爬行的最短路程即为线段![]() 的长)
的长)
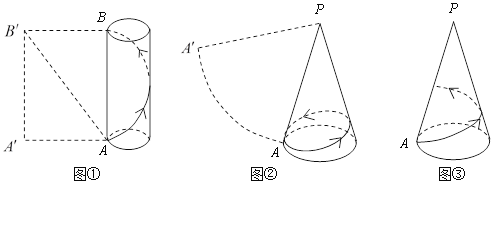
(2)如图②所示是一个底面半径为![]() ,母线长为4的圆锥和它的侧面展开图,PA是它的一条母线,一只蚂蚁从A点出发沿圆锥的侧面爬行一周后回到A点,求蚂蚁爬行的最短路程.
,母线长为4的圆锥和它的侧面展开图,PA是它的一条母线,一只蚂蚁从A点出发沿圆锥的侧面爬行一周后回到A点,求蚂蚁爬行的最短路程.
(3)如图③所示,在②的条件下,一只蚂蚁从A点出发沿圆锥的侧面爬行一周到达母线PA上的一点,求蚂蚁爬行的最短路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为t秒.
(1)当t=2时,则AP= ,此时点P的坐标是 。
(2)当t=3时,求过点P的直线l:y=-x+b的解析式?
(3)当直线l:y=-x+b从经过点M到点N时,求此时点P向上移动多少秒?
(4)点Q在x轴时,若S△ONQ=8时,请直按写出点Q的坐标是 。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M为抛物线![]() 与x轴的焦点为A(-3,0),B(1,0),与y轴交于点C,连结AM,AC,点D为线段AM上一动点(不与A重合),以CD为斜边在CD上侧作等腰Rt△DEC,连结AE,OE.
与x轴的焦点为A(-3,0),B(1,0),与y轴交于点C,连结AM,AC,点D为线段AM上一动点(不与A重合),以CD为斜边在CD上侧作等腰Rt△DEC,连结AE,OE.
(1)求抛物线的解析式及顶点M的坐标;
(2)求解AD:OE的值;
(3)当△OEC为直角三角形时,求AD的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com