
【题目】某企业有甲、乙两个长方体的蓄水池,将甲池中的水以每小时6立方米的速度注入乙池,甲、乙两个蓄水池中水的深度y(米)与注水时间x(时)之间的函数图象如图所示,结合图象回答下列问题:
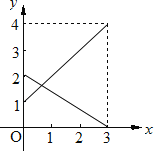
(1)分别求出甲、乙两个蓄水池中水的深度y与注水时间x之间的函数关系式;
(2)求注水多长时间甲、乙两个蓄水池水的深度相同;
(3)求注水多长时间甲、乙两个蓄水池的蓄水量相同.
【答案】(1)甲:y=-![]() x+2 乙:y=x+1 (2)x=0.6 (3)1小时.
x+2 乙:y=x+1 (2)x=0.6 (3)1小时.
【解析】
(1)利用待定系数法进行求解;
(2)当y相等时列出x的方程,然后进行求解;
(3)分别设两个蓄水池的底面积,然后根据体积相等进行求解.
(1)甲蓄水池中水的深度y与注水时间x之间的函数关系式为:y=-![]() x+2
x+2
乙蓄水池中水的深度y与注水时间x之间的函数关系式为:y=x+1
(2) 当-![]() x+2=x+1时, 解得:x=0.6;
x+2=x+1时, 解得:x=0.6;
(3)设甲蓄水池的底面积为![]() ,乙蓄水池的底面积为
,乙蓄水池的底面积为![]() ,t小时甲、乙两个蓄水池的蓄水量相同.
,t小时甲、乙两个蓄水池的蓄水量相同.
∵甲水深度下降2米,而乙水池深度升高3米,所以甲乙两水池的底面积比是3:2,
∴2![]() =3×6, ∴S1=9, ∵(4-1)
=3×6, ∴S1=9, ∵(4-1)![]() =3×6, ∴
=3×6, ∴![]() =6,
=6,
∵![]() (-
(-![]() x+2)=
x+2)=![]() (t+1) 解得t=1.
(t+1) 解得t=1.
∴注水1小时甲、乙两个蓄水池的蓄水量相同.


科目:初中数学 来源: 题型:
【题目】季末打折促销,甲乙两商场促销方式不同,两商场实际付费![]() (元)与标价
(元)与标价![]() (元)之间的函数关系如图所示折线
(元)之间的函数关系如图所示折线![]() (虚线)表示甲商场,折线
(虚线)表示甲商场,折线![]() 表示乙商场
表示乙商场
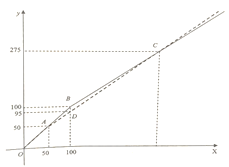
(1)分别求射线![]() 的解析式.
的解析式.
(2)张华说他必须选择乙商场,由此推理张华计划购物所需费用![]() (元)(标价)的范围是______.
(元)(标价)的范围是______.
(3)李明说他必须选择甲商场,由此推理李明计划购物所需费用![]() (元)(标价)的范围是______.
(元)(标价)的范围是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张先生准备租一处临街房屋开一家电脑公司,现有甲乙两家房屋 出租,甲屋已装修好,每月租金3000元,乙屋没有装修,每月租金2000元,但要装修成甲屋的模样,需要花费4万元,如果你是张先生,你会如何选择?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位急需用车,但又不准备买车,他们准备和一个体车主或一国营出租车公司其中的一家签订月租车合同.设汽车每月行驶xkm,应付给个体车主的月租费用是y1元,应付给出租公司的月租费用是y2元,y1、y2分别与x之间的函数关系图像(两条射线)如图所示,观察图像回答下列问题:
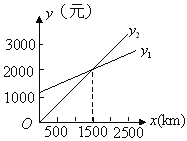
(1)每月行驶的路程在什么范围内时,租国有公司的车合算?
(2)每月行驶的路程等于多少时,租两家车的费用相同?
(3)如果这个单位估计每月行驶的路程为2300km,那么这个单位租哪家的车合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2﹣2x+3与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1关于点B中心对称得C2,C2与x轴交于另一点C,将C2关于点C中心对称得C3,连接C1与C3的顶点,则图中阴影部分的面积为_________.
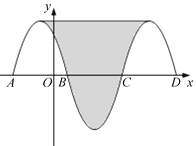
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某村庄计划建造A,B两种型号的沼气池共20个,以解决该村所有农户的燃料问题.两种型号沼气池的占地面积和可供使用农户数见下表:
型号 | 占地面积 (单位:m2/个) | 可供使用农户数 (单位:户/个) |
A | 15 | 18 |
B | 20 | 30 |
已知可供建造沼气池的占地面积不超过365m2,该村农户共有492户.
(1)如何合理分配建造A,B型号“沼气池”的个数才能满足条件?满足条件的方案有几种?通过计算分别写出各种方案.
(2)请写出建造A、B两种型号的“沼气池”的总费用y和建造A型“沼气池”个数x之间的函数关系式;
(3)若A型号“沼气池”每个造价2万元,B型号“沼气池”每个造价3万元,试说明在(1)中的各种建造方案中,哪种建造方案最省钱,最少的费用需要多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嫦娥四号探测器于2019年1月3日,成功着陆在月球背面,通过“鹊桥”中继星传回了世界第一张近距离拍摄的月背影像图,开启了人类月球探测新篇章.当中继星成功运行于地月拉格朗日L2点时,它距离地球约1500000km.用科学记数法表示数1500000为( )

A. 15×105 B. 1.5×106 C. 0.15×107 D. 1.5×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某公司计划用32m长的材料沿墙建造的长方形仓库,仓库的一边靠墙,已知墙长16m,设长方形的宽AB为xm.

(1)用x的代数式表示长方形的长BC;
(2)能否建造成面积为120㎡的长方形仓库?若能,求出长方形仓库的长和宽;若不能,请说明理由;
(3)能否建造成面积为160㎡的长方形仓库?若能,求出长方形仓库的长和宽;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com