
ШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxoyжаЃЌжБЯп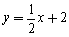 гыx жсНЛгкЕуAЃЌгыyжсНЛгкЕуCЃЎХзЮяЯпy=ax2+bx+cЕФЖдГЦжсЪЧ
гыx жсНЛгкЕуAЃЌгыyжсНЛгкЕуCЃЎХзЮяЯпy=ax2+bx+cЕФЖдГЦжсЪЧ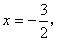 ЧвОЙ§AЁЂCСНЕуЃЌгыxжсЕФСэвЛНЛЕуЮЊЕуBЃЎ
ЧвОЙ§AЁЂCСНЕуЃЌгыxжсЕФСэвЛНЛЕуЮЊЕуBЃЎ
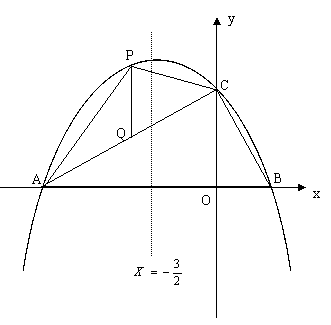
ЃЈ1ЃЉЃЈ4ЗжЃЉЂйжБНгаДГіЕуBЕФзјБъЃЛЂкЧѓХзЮяЯпНтЮіЪНЃЎ
ЃЈ2ЃЉЃЈ4ЗжЃЉШєЕуPЮЊжБЯпACЩЯЗНЕФХзЮяЯпЩЯЕФвЛЕуЃЌСЌНгPAЃЌPCЃЎЧѓЁїPACЕФУцЛ§ЕФзюДѓжЕЃЌВЂЧѓГіДЫЪБЕуPЕФзјБъЃЎ
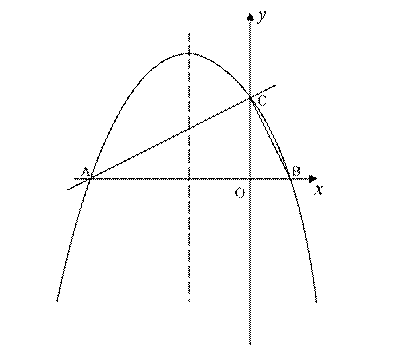 ЃЈ3ЃЉЃЈ4ЗжЃЉХзЮяЯпЩЯЪЧЗёДцдкЕуMЃЌЙ§ЕуMзїMNДЙжБxжсгкЕуNЃЌЪЙЕУвдЕуAЁЂMЁЂNЮЊЖЅЕуЕФШ§НЧаЮгыЁїABCЯрЫЦЃПШєДцдкЃЌЧѓГіЕуMЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ3ЃЉЃЈ4ЗжЃЉХзЮяЯпЩЯЪЧЗёДцдкЕуMЃЌЙ§ЕуMзїMNДЙжБxжсгкЕуNЃЌЪЙЕУвдЕуAЁЂMЁЂNЮЊЖЅЕуЕФШ§НЧаЮгыЁїABCЯрЫЦЃПШєДцдкЃЌЧѓГіЕуMЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
|

(1) ЂйB(1,0)
(2)
Ђкy=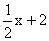 ЕБx=0ЪБЃЌyЃН2, ЕБy=0ЪБЃЌx=Ѓ4
ЕБx=0ЪБЃЌyЃН2, ЕБy=0ЪБЃЌx=Ѓ4
Ёр C(0,2),A(Ѓ4,0) ЁпХзЮяЯпy=ax2+bx+cЙ§A(Ѓ4,0), B(1,0)
ЁрПЩЩшХзЮяЯпНтЮіЪНЮЊy=a(x+4)(xЃ1)
 гжЁпХзЮяЯпЙ§ЕуC(0,2) Ёр2=Ѓ4a Ёрa=
гжЁпХзЮяЯпЙ§ЕуC(0,2) Ёр2=Ѓ4a Ёрa=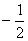
Ёрy=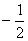 x2
x2 x+2
x+2
(2)ЩшPЃЈm,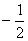 m2
m2 m+2).
m+2).
Й§ЕуPзїPQЁЭxжсНЛACгкЕуQ
ЁрQ(m, m+2)
m+2)
ЁрPQ=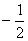 m2
m2 m+2Ѓ(
m+2Ѓ( m+2)
m+2)
=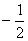 m2Ѓ2m
m2Ѓ2m
Ёп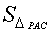 =
=
 PQ
PQ 4
4
 =2PQ=Ѓm2Ѓ4m=Ѓ(m+2)2+4
=2PQ=Ѓm2Ѓ4m=Ѓ(m+2)2+4
ЁрЕБm=Ѓ2ЪБЃЌІЄPACЕФУцЛ§газюДѓжЕЪЧ4
ДЫЪБPЃЈЃ2ЃЌ3ЃЉ
ЃЈ3ЃЉдкRtІЄAOCжаЃЌtanЁЯCAO= дкRtІЄBOCжаЃЌtanЁЯBCO=
дкRtІЄBOCжаЃЌtanЁЯBCO=
ЁрЁЯCAO=ЁЯBCO ЁпЁЯBCO+ЁЯOBC=90Ёу
ЁрЁЯCAO+ЁЯOBC=90Ёу ЁрЁЯACB=90Ёу
Ёр ІЄABCЁзІЄACOЁзІЄCBO
Ђй ЕБMЕугыCЕужиКЯЃЌМДMЃЈ0ЃЌ2ЃЉЪБЃЌІЄMANЁзІЄBAC
Ђк ИљОнХзЮяЯпЕФЖдГЦадЃЌЕБM(Ѓ3,2) ЪБЃЌІЄMANЁзІЄABC
Ђл ЕБЕуMдкЕкЫФЯѓЯоЪБЃЌЩшMЃЈn,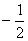 n2
n2 n+2ЃЉЃЌдђN(n,0)
n+2ЃЉЃЌдђN(n,0)
Ёр MN= n2+
n2+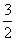 nЃ2 , AN=n+4
nЃ2 , AN=n+4
ЕБ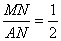 ЪБЃЌMN=
ЪБЃЌMN= AN МД
AN МД n2+
n2+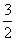 nЃ2=
nЃ2= (n+4)
(n+4)
n2+2nЃ8=0 Ёр n1= Ѓ4(Щс), n2=2
ЁрMЃЈ2ЃЌЃ3ЃЉ
ЕБ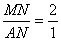 ЪБЃЌMN=2AN
ЪБЃЌMN=2AN  n2+
n2+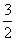 nЃ2=2(n+4)
nЃ2=2(n+4)
n2ЃnЃ20=0 Ёр n1= Ѓ4(Щс), n2=5
ЁрMЃЈ5ЃЌЃ18ЃЉ
злЩЯЫљЪіЃКДцдкM1ЃЈ0ЃЌ2ЃЉ,M2(Ѓ3,2), M3ЃЈ2ЃЌЃ3ЃЉ,M4ЃЈ5ЃЌЃ18ЃЉ, ЪЙЕУвдЕу
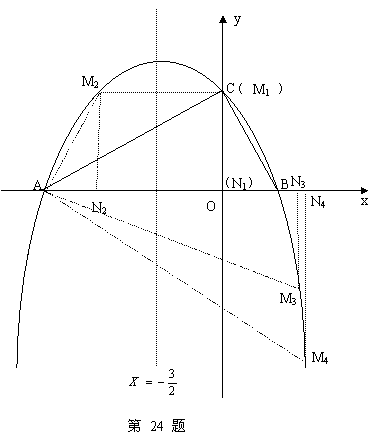 AЁЂMЁЂNЮЊЖЅЕуЕФШ§НЧаЮгыЁїABCЯрЫЦ.
AЁЂMЁЂNЮЊЖЅЕуЕФШ§НЧаЮгыЁїABCЯрЫЦ.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
дкЦНУцжБНЧзјБъЯЕжаЃЌШєжБЯп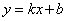 ОЙ§ЕквЛЁЂШ§ЁЂЫФЯѓЯоЃЌдђжБЯп
ОЙ§ЕквЛЁЂШ§ЁЂЫФЯѓЯоЃЌдђжБЯп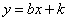 ВЛОЙ§ЕФЯѓЯоЪЧ
ВЛОЙ§ЕФЯѓЯоЪЧ
AЁЂЕквЛЯѓЯо BЁЂЕкЖўЯѓЯо CЁЂЕкШ§ЯѓЯо DЁЂЕкЫФЯѓЯо
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
дкЦНааЫФБпаЮABCDжаЃЌEЮЊBCБпЩЯЕФвЛЕу.СЌНсAE.
ЃЈ1ЃЉШєAB=AE, ЧѓжЄ:ЁЯDAE=ЁЯDЃЛ
ЃЈ2ЃЉШєЕуEЮЊBCЕФжаЕуЃЌСЌНгBDЃЌНЛAEгкF,ЧѓEF︰FAЕФжЕ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
АЫФъМЖЃЈ1ЃЉАрбЇЩњдкЭъГЩПЮЬтбЇЯАЁАЬхжЪНЁПЕВтЪджаЕФЪ§ОнЗжЮіЁБ
КѓЃЌРћгУПЮ ЭтЛюЖЏЪБМфЛ§МЋВЮМгЬхг§ЖЭСЖЃЌУПЮЛЭЌбЇДгРКЧђЁЂЬјЩўЁЂСЂЖЈЬјдЖЁЂГЄХмЁЂЧІЧђжабЁвЛЯюНјаабЕСЗЃЌбЕСЗКѓЖМНјааСЫВтЪдЃЎЯжНЋЯюФПбЁдёЧщПіМАбЕСЗКѓРКЧђЖЈЪБЖЈЕуЭЖРКВтЪдГЩМЈећРэКѓзїГіШчЯТЭГМЦЭМЃЎ
ЭтЛюЖЏЪБМфЛ§МЋВЮМгЬхг§ЖЭСЖЃЌУПЮЛЭЌбЇДгРКЧђЁЂЬјЩўЁЂСЂЖЈЬјдЖЁЂГЄХмЁЂЧІЧђжабЁвЛЯюНјаабЕСЗЃЌбЕСЗКѓЖМНјааСЫВтЪдЃЎЯжНЋЯюФПбЁдёЧщПіМАбЕСЗКѓРКЧђЖЈЪБЖЈЕуЭЖРКВтЪдГЩМЈећРэКѓзїГіШчЯТЭГМЦЭМЃЎ
ЯюФПбЁдёШЫЪ§ЧщПіЭГМЦЭМ бЕСЗКѓРКЧђЖЈЪБЖЈЕуЭЖРКВтЪдНјЧђЪ§ЭГМЦЭМ
 | |||
 | |||
ЧыФуИљОнЩЯУцЬсЙЉЕФаХЯЂЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЃЈ3ЗжЃЉЩШаЮЭМжаЬјЩўВПЗжЕФЩШаЮдВаФНЧЮЊ  ЖШЃЌИУАрЙВгабЇЩњ ШЫЃЌ
ЖШЃЌИУАрЙВгабЇЩњ ШЫЃЌ
бЕСЗКѓРКЧђЖЈЪБЖЈ ЕуЭЖРКЦНОљУПИіШЫЕФНјЧђЪ§ЪЧ ЃЎ
ЕуЭЖРКЦНОљУПИіШЫЕФНјЧђЪ§ЪЧ ЃЎ
ЃЈ2ЃЉЃЈ5ЗжЃЉРЯЪІОіЖЈДгбЁдёЧІЧђбЕСЗЕФ3УћФаЩњКЭ1УћХЎЩњжаШЮбЁСНУћбЇЩњЯШНјааВтЪдЃЌЧыгУСаБэЛђЛЪїаЮЭМЕФЗНЗЈЧѓЧЁКУбЁжаСНУћФаЩњЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЯТСаГЄЖШЕФШ§ЬѕЯпЖЮФмзщГЩШ§НЧаЮЕФЪЧЃЈЁЁЁЁЃЉ
A. 1,2,3 B.,1ЃЌ ЃЌ3 C.3,4,8 D.4,5ЃЌ6
ЃЌ3 C.3,4,8 D.4,5ЃЌ6
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
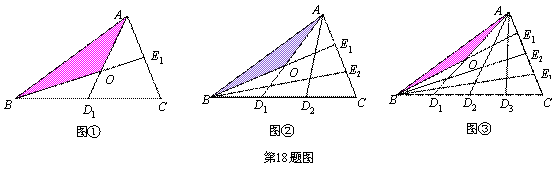
ЩшЁїABCЕФУцЛ§ЮЊ1ЃЌШчЭМЂйНЋБпBCЁЂACЗжБ№2ЕШЗнЃЌ ЁЂ
ЁЂ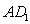 ЯрНЛгкЕуOЃЌЁїAOBЕФУцЛ§МЧЮЊ
ЯрНЛгкЕуOЃЌЁїAOBЕФУцЛ§МЧЮЊ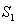 ЃЛШчЭМЂкНЋБпBCЁЂACЗжБ№3ЕШЗнЃЌ
ЃЛШчЭМЂкНЋБпBCЁЂACЗжБ№3ЕШЗнЃЌ ЁЂ
ЁЂ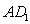 ЯрНЛгкЕуOЃЌЁїAOBЕФУцЛ§МЧЮЊ
ЯрНЛгкЕуOЃЌЁїAOBЕФУцЛ§МЧЮЊ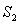 ЃЛЁЁЃЌ вРДЫРрЭЦЃЌдђ
ЃЛЁЁЃЌ вРДЫРрЭЦЃЌдђ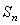 ПЩБэЪОЮЊ .(гУКЌ
ПЩБэЪОЮЊ .(гУКЌ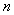 ЕФДњЪ§ЪНБэЪОЃЌЦфжа
ЕФДњЪ§ЪНБэЪОЃЌЦфжа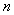 ЮЊе§ећЪ§)
ЮЊе§ећЪ§)
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com