
【题目】如图,平行四边形ABCD中,点E是BC边上的中点,过A作AF⊥CD,AE⊥EF.
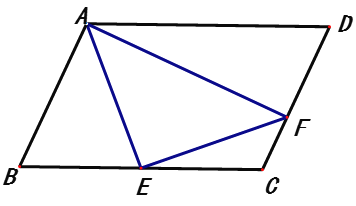
(1)若∠B=60°,AE平分∠BAF,DF=4.求AE的长.
(2)求证:AB+CF=![]() EF
EF
【答案】(1)2![]() ;(2)详见解析;
;(2)详见解析;
【解析】
(1)首先根据含30°直角三角形的性质求出AF,然后证明∠EAF=45°,利用三角函数求AE即可;
(2)取AF中点G,连接EG,根据中位线的性质可得EG∥CD,AB+CF=2EG,然后根据直角三角形的性质可得EG=GF,证明△GEF是等腰直角三角形即可.
解:(1)∵在平行四边形ABCD中,∠B=60°,DF=4,
∴∠D=60°,∠BAD=120°,
∵AF⊥CD,
∴∠DAF=30°,AF=![]() DF=
DF=![]() ,
,
∴∠BAF=90°,
∴∠EAF=45°,
∵AE⊥EF,
∴AE=AF·cos45°=![]() ;
;
(2)取AF中点G,连接EG,
∵点E是BC边上的中点,
∴EG∥CD,EG=![]() (AB+CF),即AB+CF=2EG,
(AB+CF),即AB+CF=2EG,
∵△AEF是直角三角形,
∴EG=GF,
∵AF⊥CD,
∴EG⊥AF,
∴ △GEF是等腰直角三角形,
∴EF=![]() EG,
EG,
∴AB+CF=![]() EF.
EF.



 每课必练系列答案
每课必练系列答案科目:初中数学 来源: 题型:
【题目】已知:如图所示,在△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.
(1)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ的面积等于4cm2?
(2)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ中PQ的长度等于5cm?
(3)在(1)中,当P,Q出发几秒时,△PBQ有最大面积?
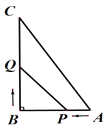
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,将![]() 沿弦BC所在直线折叠,折叠后的弧与直径AB相交于点D,连接CD.
沿弦BC所在直线折叠,折叠后的弧与直径AB相交于点D,连接CD.
(1)若点D恰好与点O重合,则∠ABC= °;
(2)延长CD交⊙O于点M,连接BM.猜想∠ABC与∠ABM的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
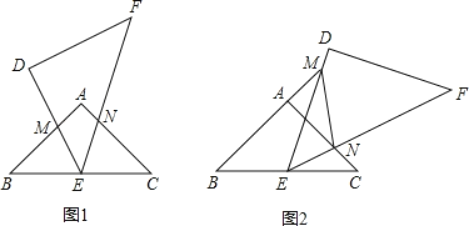
【题目】△ABC和△DEF是两个等腰直角三角形,∠A=∠D=90°,△DEF的顶点E位于边BC的中点上.
(1)如图1,设DE与AB交于点M,EF与AC交于点N,求证:△BEM∽△CNE;
(2)如图2,将△DEF绕点E旋转,使得DE与BA的延长线交于点M,EF与AC交于点N,于是,除(1)中的一对相似三角形外,能否再找出一对相似三角形并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】蜂蜜具有消食、润肺、安神、美颜之功效,是天然的健康保健佳品.秋天即将来临时,雪宝山土特产公司抓住商机购进甲、乙、丙三种蜂蜜,已知销售每瓶甲蜂蜜的利润率为10%,每瓶乙蜂蜜的利润率为20%,每瓶丙蜂蜜的利润率为30%.当售出的甲、乙、丙蜂蜜瓶数之比为1:3:1时,商人得到的总利润率为22%;当售出的甲、乙、丙蜂蜜瓶数之比为3:2:1时,商人得到的总利润率为20%.那么当售出的甲、乙、丙蜂蜜瓶数之比为5:6:1时,该公司得到的总利润率为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,防洪大堤的横截面ABGH是梯形,背水坡AB的坡度i=1:![]() (垂直高度AE与水平宽度BE的比),AB=20米,BC=30米,身高为1.7米的小明(AM=1.7米)站在大堤A点(M,A,E三点在同一条直线上),测得电线杆顶端D的仰角∠
(垂直高度AE与水平宽度BE的比),AB=20米,BC=30米,身高为1.7米的小明(AM=1.7米)站在大堤A点(M,A,E三点在同一条直线上),测得电线杆顶端D的仰角∠![]() =20°.
=20°.
(1)求∠ABC;
(2)求电线杆CD的高度.(结果精确到个位,参考数据sin20°≈0.3,cos20°≈0.9,tan20°≈0.4,![]() ≈1.7)
≈1.7)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四张质地相同的卡片如图所示.将卡片洗匀后,背面朝上放置在桌面上.

(1)求随机抽取一张卡片,恰好得到数字2的概率;
(2)小贝和小晶想用以上四张卡片做游戏,游戏规则见信息图.你认为这个游戏公平吗?请用列表法或画树形图法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.
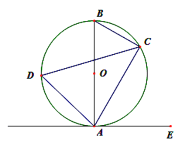
(1)求证:AE是⊙O的切线;
(2) 连接OC,当BC=3时,求劣弧AC的长和扇形B0C的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com