
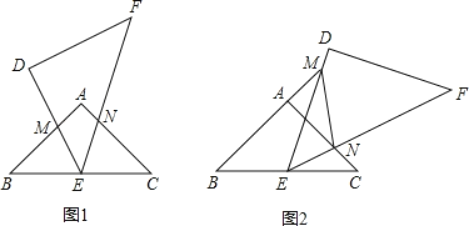
【题目】△ABC和△DEF是两个等腰直角三角形,∠A=∠D=90°,△DEF的顶点E位于边BC的中点上.
(1)如图1,设DE与AB交于点M,EF与AC交于点N,求证:△BEM∽△CNE;
(2)如图2,将△DEF绕点E旋转,使得DE与BA的延长线交于点M,EF与AC交于点N,于是,除(1)中的一对相似三角形外,能否再找出一对相似三角形并证明你的结论.
【答案】(1)见解析,(2)能,△ECN∽△MEN,见解析.
【解析】
(1)由△ABC和△DEF是两个等腰直角三角形,易得∠BME=∠NEC,又由∠B=∠C=45°,即可证得△BEM∽△CNE;
(2)与(1)同理△BEM∽△CNE,可得![]() ,又由BE=EC,即可得
,又由BE=EC,即可得![]() ,然后由∠ECN=∠MEN=45°,证得△ECN∽△MEN.
,然后由∠ECN=∠MEN=45°,证得△ECN∽△MEN.
证明:(1)∵△ABC是等腰直角三角形,
∴∠MBE=45°,∴∠BME+∠MEB=135°
又∵△DEF是等腰直角三角形,∴∠DEF=45°
∴∠NEC+∠MEB=135°
∴∠BME=∠NEC,
而∠B=∠C=45°,
∴△BEM∽△CNE.
(2)与(1)同理△BEM∽△CNE,
∴![]() .
.
又∵BE=EC,
∴![]() ,
,
在△ECN与△MEN中有![]() ,
,
又∠ECN=∠MEN=45°,
∴△ECN∽△MEN.


科目:初中数学 来源: 题型:
【题目】如图所示.在△ABC中,内角∠BAC与外角∠CBE的平分线相交于点P,BE=BC,PB与CE交于点H,PG∥AD交BC于F,交AB于G,连接CP.下列结论:①∠ACB=2∠APB;②S△PAC:S△PAB=AC:AB;③BP垂直平分CE;④∠PCF=∠CPF.其中,正确的有( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
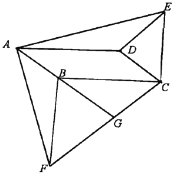
【题目】如图,在口ABCD中,分别以边BC,CD作等腰△BCF,△CDE,使BC=BF,CD=DE,∠CBF=∠CDE,连接AF,AE.
(1)求证:△ABF≌△EDA;
(2)延长AB与CF相交于G,若AF⊥AE,求证BF⊥BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
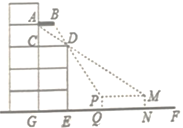
【题目】周末,小凯和同学带着皮尺,去测量杨大爷家露台遮阳蓬的宽度,如图,由于无法直接测量,小凯便在楼前面的地面上选择了一条直线EF,通过在直线EF上选点观测,发现当他位于N点时,他的视线从M点通过露台D点正好落在遮阳蓬A点处:当他位于Q点时,视线从P点通过露台D点正好落在遮阳蓬B点处,这样观测到两个点A,B间的距离即为遮阳蓬的宽.已知AB∥CD∥EF,点C在AG上,AG、DE、PQ、MN均为垂直于EF,MN=PQ,露台的宽CD=GE,测得GE=5米,EN=13.2米,QN=6.2,请你根据以上信息,求出遮阳蓬的宽AB是多少米?(结果精确到0.01米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,顶点坐标为(﹣2,﹣9a),下列结论:①4a+2b+c>0;②5a﹣b+c=0;③若方程a(x+5)(x﹣1)=﹣1有两个根x1和x2,且x1<x2,则﹣5<x1<x2<1;④若方程|ax2+bx+c|=1有四个根,则这四个根的和为﹣4.其中正确的结论有( )
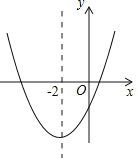
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1.
①b2>4ac;
②4a﹣2b+c<0;
③不等式ax2+bx+c>0的解集是x≥3.5;
④若(﹣2,y1),(5,y2)是抛物线上的两点,则y1<y2.
上述4个判断中,正确的是( )

A.①② B.①④ C.①③④ D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=30°,B为OM上一点,BA⊥ON于点A,四边形ABCD为正方形,P为射线BM上一动点,连结CP,将CP绕点C顺时针方向旋转90°得CE,连接BE,若AB=2,则BE的最小值为( )
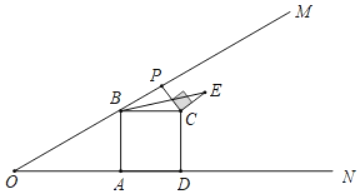
A. ![]() +1B. 2
+1B. 2![]() ﹣1C. 3D. 4﹣
﹣1C. 3D. 4﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=ax2﹣3(a+1)x+2a+3(a≠0)与直线y=x﹣1交于点A和点B(点A在点B的左侧),AB=5![]() .
.
(1)求证:该抛物线必过一个定点;
(2)求该抛物线的解析式;
(3)设直线x=m与该抛物线交于点E(x1,y1),与直线AB交于点F(x2,y2),当满足y1+y2>0且y1y2<0时,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
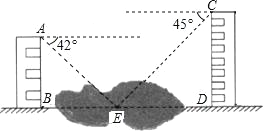
【题目】如图,两幢建筑物AB和CD,AB⊥BD,CD⊥BD,AB=15m,CD=20m.AB和CD之间有一景观池,小双在A点测得池中喷泉处E点的俯角为42°,在C点测得E点的俯角为45°,点B、E、D在同一直线上.求两幢建筑物之间的距离BD.(结果精确到0.1m)(参考数据:sin42°=0.67,cos42°=0.74,tan42°=0.90)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com