
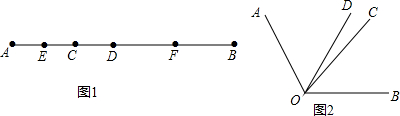
分析 (1)根据线段中点的定义可以求得EC=$\frac{1}{2}$AC,DF=$\frac{1}{2}$BD,则EF=EC+CD+DF;(2)设∠BOC=x,然后用x与∠COD的度数分别表示出∠AOD与∠BOD,然后根据角平分线的定义可知∠AOD=∠BOD,计算即可求出x的值,然后求出∠AOC与∠BOC的度数,相加即可得解.
解答 解:(1):∵AB=20,CD=8,
∴AC+BD=AB-CD=12.
∵E为AC中点,F为BD中点,
∴EC=$\frac{1}{2}$AC,DF=$\frac{1}{2}$BD,
∴EF=EC+CD+DF=$\frac{1}{2}$(AC+BD)+CD=$\frac{1}{2}$×12+8=14;
(2)设∠BOC=x,则∠AOC=2x,
∵∠COD=21°30′,
∴∠AOD=2x-21°30′,∠BOD=x+21°30′,
∵OD是∠AOB的平分线,
∴∠AOD=∠BOD,
∴2x-21°30′=x+21°30′,
解得x=43°,
∴2x=2×43°=86°,
即∠AOC=86°,∠BOC=43°,
∴∠AOB=∠AOC+∠BOC=86°+43°=129°.
点评 (1)题考查了两点间的距离.连接两点的连线段的长度叫这两点间的距离.也考查了线段中点的定义;(2)题主要考查了角度的计算,角平分线的定义,分别表示出∠AOD与∠BOD是解题的关键,需要注意度、分、秒是60进制,计算时不要出错


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 时钟的分针每分钟转过的角度是6°,时针每分钟转过的角度是$\frac{1}{2}$°.今天我们数学考试的时间是13﹕00--14﹕30,在这一个半小时的时间内,时针与分针所夹的角将有几个时刻为36°?试分别求出这几个时刻.
时钟的分针每分钟转过的角度是6°,时针每分钟转过的角度是$\frac{1}{2}$°.今天我们数学考试的时间是13﹕00--14﹕30,在这一个半小时的时间内,时针与分针所夹的角将有几个时刻为36°?试分别求出这几个时刻.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com