
【题目】一艘在南北航线上的测量船,于A点处测得海岛B在点A的南偏东30°方向,继续向南航行30海里到达C点时,测得海岛B在C点的北偏东15°方向,那么海岛B离此航线的最近距离是(结果保留小数点后两位)(参考数据:![]() )( )
)( )
A. 4.64海里 B. 5.49海里 C. 6.12海里 D. 6.21海里
【答案】B
【解析】
根据题意画出图如图所示:作BD⊥AC,取BE=CE,根据三角形内角和和等腰三角形的性质得出BA=BE,AD=DE,设BD=x,Rt△ABD中,根据勾股定理得AD=DE=![]() x,AB=BE=CE=2x,由AC=AD+DE+EC=2
x,AB=BE=CE=2x,由AC=AD+DE+EC=2![]() x+2x=30,解之即可得出答案.
x+2x=30,解之即可得出答案.
根据题意画出图如图所示:作BD⊥AC,取BE=CE,
∵AC=30,∠CAB=30°∠ACB=15°,
∴∠ABC=135°,
又∵BE=CE,
∴∠ACB=∠EBC=15°,
∴∠ABE=120°,
又∵∠CAB=30°
∴BA=BE,AD=DE,
设BD=x,
在Rt△ABD中,
∴AD=DE=![]() x,AB=BE=CE=2x,
x,AB=BE=CE=2x,
∴AC=AD+DE+EC=2![]() x+2x=30,
x+2x=30,
∴x=![]() =
=![]() ≈5.49,
≈5.49,
故答案选:B.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某工厂计划生产一种创新产品,若生产一件这种产品需A种原料1.2千克、B种原料1千克.已知A种原料每千克的价格比B种原料每千克的价格多10元.
(1)为使每件产品的成本价不超过34元,那么购入的B种原料每千克的价格最高不超过多少元?
(2)将这种产品投放市场批发销售一段时间后,为拓展销路又开展了零售业务,每件产品的零售价比批发价多30元.现用10000元通过批发价购买该产品的件数与用16000元通过零售价购买该产品的件数相同,那么这种产品的批发价是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小西“过直线外一点作这条直线的垂线”的尺规作图过程.
已知:直线l及直线l外一点P.
求作:直线PQ,使得PQ⊥l.
做法:如图,
①在直线l的异侧取一点K,以点P为圆心,PK长为半径画弧,交直线l于点A,B;
②分别以点A,B为圆心,大于![]() AB的同样长为半径画弧,两弧交于点Q(与P点不重合);
AB的同样长为半径画弧,两弧交于点Q(与P点不重合);
③作直线PQ,则直线PQ就是所求作的直线.
根据小西设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵PA= ,QA= ,
∴PQ⊥l( )(填推理的依据).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明设计的“作平行四边形的高”的尺规作图过程
已知:平行四边形ABCD.
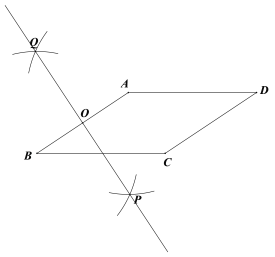
求作:![]() ,垂足为点E.
,垂足为点E.
作法:如图,
①分别以点A和点B为圆心,大于![]() 的长为半径作弧,两弧相交于P,Q两点;
的长为半径作弧,两弧相交于P,Q两点;
②作直线PQ,交AB于点O;
③以点O为圆心,OA长为半径做圆,交线段BC于点E;
④连接AE.
所以线段AE就是所求作的高.
根据小明设计的尺规作图过程
⑴使用直尺和圆规,补全图形;(保留作图痕迹)
⑵完成下面的证明
证明:![]() AP=BP, AQ= ,
AP=BP, AQ= ,
![]() PQ为线段AB的垂直平分线.
PQ为线段AB的垂直平分线.
![]() O为AB中点.
O为AB中点.
![]() AB为直径,⊙O与线段BC交于点E,
AB为直径,⊙O与线段BC交于点E,
![]()
![]()
![]() .( )(填推理的依据)
.( )(填推理的依据)
![]()
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
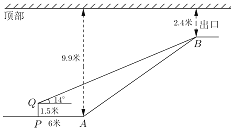
【题目】地铁10号线某站点出口横截面平面图如图所示,电梯![]() 的两端分别距顶部9.9米和2.4米,在距电梯起点
的两端分别距顶部9.9米和2.4米,在距电梯起点![]() 端6米的
端6米的![]() 处,用1.5米的测角仪测得电梯终端
处,用1.5米的测角仪测得电梯终端![]() 处的仰角为14°,求电梯
处的仰角为14°,求电梯![]() 的坡度与长度.(参考数据:
的坡度与长度.(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有大小两种货车,3辆大货车与4辆小货车一次可以运货18吨,2辆大货车与6辆小货车一次可以运货17吨.
(1)请问1辆大货车和1辆小货车一次可以分别运货多少吨?
(2)目前有33吨货物需要运输,货运公司拟安排大小货车共计10辆,全部货物一次运完,其中每辆大货车一次运费花费130元,每辆小货车一次运货花费100元,请问货运公司应如何安排车辆最节省费用?
查看答案和解析>>
科目:初中数学 来源: 题型:
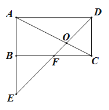
【题目】如图所示,在矩形ABCD中,点F是 BC的中点,DF的延长线与AB的延长线相交于点E,DE与AC相交于点O,若![]() ,则
,则![]() ( )
( )
A. 4 B. 6 C. 8 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
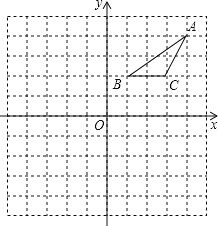
【题目】在正方形网格中建立如图所示的平面直角坐标系xOy.△ABC的三个顶点都在格点上,点A、B、C的坐标分别是A(4,4)、B(1,2)、C(3,2),请解答下列问题.
(1)将△ABC向下平移5个单位长度,画出平移后的△A1B1C1;
(2)画出△A1B1C1关于y轴对称的△A2B2C2;
(3)将△ABC绕点O逆时针旋转90°,画出旋转后的△A3B3C3.并写出点A3的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解下列方程,其中应在方程左右两边同时加上4的是( )
A. x2﹣2x=5 B. x2+4x=5 C. 2x2﹣4x=5 D. 4x2+4x=5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com