
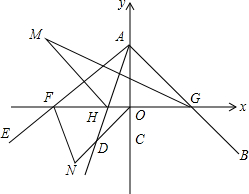
 如图,平面直角坐标系中,∠BAC=45°,AC在y轴上,∠DAE=35°,AE,AB,AD分别交x轴于点F、G、H.在∠DAE旋转过程中,设AE交x轴于F,∠AGH的平分线与∠AHF的平分线交于点M,∠COF的平分线与∠OFE的平分线交于点N.下列两个结论:①∠N+∠M为定值;②∠N-∠M为定值.其中有且仅有一个是正确的,请你选出正确的结论,并求出其值.
如图,平面直角坐标系中,∠BAC=45°,AC在y轴上,∠DAE=35°,AE,AB,AD分别交x轴于点F、G、H.在∠DAE旋转过程中,设AE交x轴于F,∠AGH的平分线与∠AHF的平分线交于点M,∠COF的平分线与∠OFE的平分线交于点N.下列两个结论:①∠N+∠M为定值;②∠N-∠M为定值.其中有且仅有一个是正确的,请你选出正确的结论,并求出其值. 分析 根据角平分线的性质和三角形的内角和,可证当改变α的大小时,∠N+∠M的值不会改变.
解答 解:①∠N+∠M为定值;
设∠HAC=α,∠GAO=∠AGO=45°,
∴∠FHA=∠HAG+∠AGH=90°+α.
∵HM平分∠AHF,
∴∠FHM=$\frac{1}{2}$∠FHA=45°+$\frac{1}{2}$α.
∵GM平分∠AGH,
∴∠HGM=$\frac{1}{2}$∠AGO=22.5°.
∵∠FHM=∠HMG+∠MGH,
∴45°+$\frac{1}{2}$α=∠M+22.5°,
∴∠M=22.5°+$\frac{1}{2}$α.
又∵FN平分∠EFO,
∴∠NFO=$\frac{1}{2}$∠EFO=$\frac{1}{2}$(∠FOA+∠FAO)=$\frac{1}{2}$(90°+35°+α)=62.5°+$\frac{1}{2}$α,
∴∠N=180°-∠NFO-∠NOF
=180°-(62.5°+$\frac{1}{2}$α)-45°
=72.5°-$\frac{1}{2}$α.
∴∠N+∠M=(72.5°-$\frac{1}{2}$α)+(22.5°+$\frac{1}{2}$α)=95°.
点评 本题主要考查三角形的内角和、坐标与图形的性质、平行线的性质、三角形的面积;难点在于看懂已知的图形,根据已知条件,充分挖掘隐含的条件.此类题学生丢分率较高,需注意.


科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,AB=6,∠B=60°,以BC所在直线为x轴,以B点为原点建立直角坐标系,则点A的坐标是( )
如图,在△ABC中,AB=6,∠B=60°,以BC所在直线为x轴,以B点为原点建立直角坐标系,则点A的坐标是( )| A. | (3,3) | B. | (3$\sqrt{3}$,3) | C. | (3,$3\sqrt{3}$) | D. | (3$\sqrt{3}$,3$\sqrt{3}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,直线a经过正方形ABCD的顶点A,分别过此正方形的顶点B、D作BF⊥a于点F、DE⊥a于点E,若DE=3,BF=2,则正方形ABCD的面积为13.
如图所示,直线a经过正方形ABCD的顶点A,分别过此正方形的顶点B、D作BF⊥a于点F、DE⊥a于点E,若DE=3,BF=2,则正方形ABCD的面积为13.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com