
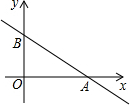
 如图:直线y=kx+3与x轴、y轴分别交于A、B两点,tan∠OAB=$\frac{3}{4}$,点C(x,y)是直线y=kx+3上与A、B不重合的动点.
如图:直线y=kx+3与x轴、y轴分别交于A、B两点,tan∠OAB=$\frac{3}{4}$,点C(x,y)是直线y=kx+3上与A、B不重合的动点.分析 (1)根据直线y=kx+3与y轴分别交于B点,以及tan∠OAB=$\frac{3}{4}$,即可得出A点坐标,从而得出一次函数的解析式;
(2)根据△AOC的面积是4,得出三角形的高,即可求出C点的坐标.
解答 解:(1)∵直线y=kx+3与y轴交于B点,
∴B(0,3),
∵tan∠OAB=$\frac{3}{4}$,
∴OA=4,
∴A(4,0),
∵直线y=kx+3过A(4,0),
∴4k+3=0,
∴k=-$\frac{3}{4}$,
∴直线的解析式为:y=-$\frac{3}{4}$x+3;
(2)∵A(4,0),
∴AO=4,
∵△AOC的面积是4,
∴△AOC的高为:2,
∴C点的纵坐标为2或-2,
∵直线的解析式为:y=-$\frac{3}{4}$x+3经过C点,
∴2=-$\frac{3}{4}$x+3,或-2=-$\frac{3}{4}$x+3,
解得x=$\frac{4}{3}$,或x=$\frac{20}{3}$
∴点C点坐标为($\frac{4}{3}$,2)或($\frac{20}{3}$,-2)时,△AOC的面积是4.
点评 此题主要考查了待定系数法求一次函数解析式以及一次函数图象上点的坐标特征,根据已知得出C点的纵坐标是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
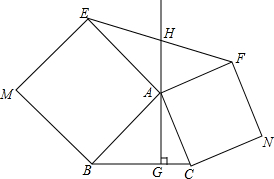 同学们小学学习了正方形,正方形就是四条边都相等,四个角都是直角.如图,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作正方形ABME和正方形ACNF,射线GA交EF于点H,试探究HE与HF之间的数量关系,并说明理由.
同学们小学学习了正方形,正方形就是四条边都相等,四个角都是直角.如图,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作正方形ABME和正方形ACNF,射线GA交EF于点H,试探究HE与HF之间的数量关系,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
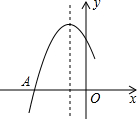 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为x=-1.与x轴的另一个交点B.给出以下几个结论:①2a-b=0;②b<0;③c>0;④b2>4ac ⑤点B的坐标是(1,0).其中正确结论的序号是①②③④⑤.
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为x=-1.与x轴的另一个交点B.给出以下几个结论:①2a-b=0;②b<0;③c>0;④b2>4ac ⑤点B的坐标是(1,0).其中正确结论的序号是①②③④⑤.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知二次函数y=x2-4x.
已知二次函数y=x2-4x.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在?ABCD中,边BC的垂直平分线EF分别交AD、BC于点M、E,交BA的延长线于点F,若点A是BF的中点,AB=5,?ABCD的周长为34,则FM的长为4.
如图,在?ABCD中,边BC的垂直平分线EF分别交AD、BC于点M、E,交BA的延长线于点F,若点A是BF的中点,AB=5,?ABCD的周长为34,则FM的长为4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com