
分析 (1)根据题意,画出图形;
(2)先过点B作BD⊥x轴于D,由A(0,2),B(5,3),即可得OA=2,BD=3,OD=5,由题意易证得△AOC∽△BDC,根据相似三角形的对应边成比例,即可得OA:BD=OC:DC=AC:BC=2:3,又由勾股定理即可求得这束光从点C到点B所经过的路径的长.
解答 解:(1)如图,
(2)过点B作BD⊥x轴于D,
∵A(0,2),B(4,3),
∴OA=2,BD=3,OD=4,
根据题意得:∠ACO=∠BCD,
∵∠AOC=∠BDC=90°,
∴△AOC∽△BDC,
∴OA:BD=OC:DC=AC:BC=2:3,
∴OC=4×$\frac{2}{5}$=1.6,
∴CD=OD-OC=2.4,
∴BC=$\sqrt{B{D}^{2}+C{D}^{2}}$=$\frac{3\sqrt{41}}{5}$.
故答案为:$\frac{3\sqrt{41}}{5}$.
点评 此题考查了相似三角形的判定与性质、勾股定理以及点与坐标的性质.解题的关键是掌握辅助线的作法,掌握入射光线与反射光线的关系.


 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
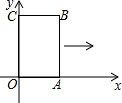 如图,矩形OABC的两条边在坐标轴上,OA=1,OC=2,现将此矩形向右平移1个单位,若平移得到的矩形的边与反比例函数图象有两个交点,它们的纵坐标之差的绝对值为0.6,求该反比例函数解析式.
如图,矩形OABC的两条边在坐标轴上,OA=1,OC=2,现将此矩形向右平移1个单位,若平移得到的矩形的边与反比例函数图象有两个交点,它们的纵坐标之差的绝对值为0.6,求该反比例函数解析式.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 “十字相乘法”能把二次三项式分解因式,对于形如ax2+bxy+cy2的x,y二次三项式来说,方法的关键是把x2项系数a分解成两个因数a1,a2的积,即a=a1•a2,把y2项系数c分解成两个因数,c1,c2的积,即c=c1•c2,并使a1•c2+a2•c1正好等于xy项的系数b,那么可以直接写成结果:ax2+bxy+cy2=(a1x+c1y)(a2x+c2y)
“十字相乘法”能把二次三项式分解因式,对于形如ax2+bxy+cy2的x,y二次三项式来说,方法的关键是把x2项系数a分解成两个因数a1,a2的积,即a=a1•a2,把y2项系数c分解成两个因数,c1,c2的积,即c=c1•c2,并使a1•c2+a2•c1正好等于xy项的系数b,那么可以直接写成结果:ax2+bxy+cy2=(a1x+c1y)(a2x+c2y)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
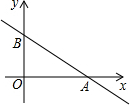 如图:直线y=kx+3与x轴、y轴分别交于A、B两点,tan∠OAB=$\frac{3}{4}$,点C(x,y)是直线y=kx+3上与A、B不重合的动点.
如图:直线y=kx+3与x轴、y轴分别交于A、B两点,tan∠OAB=$\frac{3}{4}$,点C(x,y)是直线y=kx+3上与A、B不重合的动点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
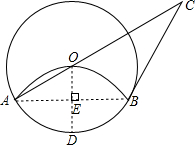 如图,将圆形纸片沿弦AB折叠后,圆弧恰好能经过圆心O,⊙O的切线BC与AO延长线交于点C.
如图,将圆形纸片沿弦AB折叠后,圆弧恰好能经过圆心O,⊙O的切线BC与AO延长线交于点C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com