Question

17．在菱形ABCD中，∠BAD=120°，射线AP位于该菱形外侧，点B关于直线AP的对称点为E，连接BE、DE，直线DE与直线AP交于F，连接BF，设∠PAB=α．
（1）依题意补全图1；
（2）如图1，如果0°＜α＜30°，判断∠ABF与∠ADF的数量关系，并证明；
（3）如图2，如果30°＜α＜60°，写出判断线段DE，BF，DF之间数量关系的思路；（可以不写出证明过程）
（4）如果60°＜α＜90°，直接写出线段DE，BF，DF之间的数量关系．

Answer 1

分析 （1）根据题目要求补全图形即可；
（2）连接AE．由轴对称图形的性质可知EA=AB，∠ABF=∠AEF，由菱形的定义可知AB=AD，从而得到AE=AD，由等腰三角形的性质可知∠AEF=∠ADF，于是得到∠ABF=∠ADF；
（3）由轴对称图形的性质可知EF=BF，然后由DF=ED-EF，可知DF=ED-BF；
（4）由轴对称图形的性质可知EF=BF，然后由EF=ED+DF，可知BF=DE+DF．

解答 解：（1）如图1所示：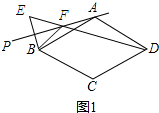

（2）∠ABF=∠ADF．
理由：如图2所示：连接AE．

∵点B与点E关于直线PA对称，
∴EA=AB，∠ABF=∠AEF．
∵四边形ABCD为菱形，
∴AB=AD．
∴AE=AD．
∴∠AEF=∠ADF．
∴∠ABF=∠ADF．
（3）DF=ED-BF．
理由：如图3所示：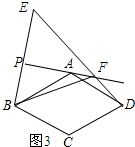

∵点B与点E关于PA对称，
∴EF=BF．
又∵DF=ED-EF，
∴DF=ED-BF．
（4）BF=DE+DF．
理由：如图4所示：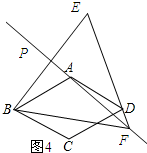

∵点B与点E关于PA对称，
∴EF=BF．
又∵EF=ED+DF，
∴BF=DE+DF．

点评 本题主要考查的是四边形的综合应用，解答本题主要应用了菱形的性质、轴对称图形的性质、等腰三角形的性质，由菱形的性质和轴对称图形的性质得到AE=AD是解题的关键．