
【题目】已知A(2,0),B(2,4),定义:若平面内点P关于直线AB的对称点Q在图形M内或图形的边界上,则称点P是图形M关于直线AB的“反称点”.
(1)已知C(5,0),D(5,3)
①点M1(0,3),M2(-0. 5,2),M3(-2,1),则是△ACD关于直线AB的“反称点”的是________:
②若直线y=2x+m上存在△ACD关于直线AB的“反称点”,求m的取值范围;
(2)已知点E(1,0),F(5,0), ![]() ,点P(x,y)在直线y=x+1上,且点P是△EFG的反称点,求点P横坐标的取值范围.
,点P(x,y)在直线y=x+1上,且点P是△EFG的反称点,求点P横坐标的取值范围.
【答案】(1)①M2;②-4≤m≤5(2)![]()
【解析】试题分析:根据“反称点”的定义解答即可.
试题解析:解:(1)①设直线AD的解析式为y=kx+b,则: ![]() ,解得:
,解得: ![]() ,∴直线AD为:y=x-2.点M1(0,3)关于直线AB的对称点为Q(4,3),当x=4时,y=x-2=2.∵2<3,∴Q在△ACD外,∴M1不是△ACD关于直线AB的“反称点”;
,∴直线AD为:y=x-2.点M1(0,3)关于直线AB的对称点为Q(4,3),当x=4时,y=x-2=2.∵2<3,∴Q在△ACD外,∴M1不是△ACD关于直线AB的“反称点”;
点M2(-0.5,2)关于直线AB的对称点为Q(4.5,2),当x=4.5时,y=x-2=2.5.∵2.5>2,∴Q在△ACD内,∴M2是△ACD关于直线AB的“反称点”;
点M3(-2,1)于直线AB的对称点为Q(6,1).∵6>5,∴Q在△ACD外,∴M3不是△ACD关于直线AB的“反称点”;
②设M(a,2a+m)在直线y=2x+m上,M关于直线AB的对称点为 Q(4-a,2a+m),则2≤4-a≤5,0≤2a+m≤2-a,解得:-1≤a≤2,-4≤m≤5;
(2)易求直线EF的解析式为![]() .点P(a,a+1)在直线y=x+1上,P关于直线AB的对称点为Q(4-a,a+1),则1≤4-a≤5,0≤a+1≤
.点P(a,a+1)在直线y=x+1上,P关于直线AB的对称点为Q(4-a,a+1),则1≤4-a≤5,0≤a+1≤![]() ,解得:-1≤a≤
,解得:-1≤a≤![]() .
.


 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】如图,圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影.已知桌面的直径为1.2 m,桌面距离地面1 m.若灯泡距离地面3 m,则地面上阴影部分的面积为 ( )

A. 0.36πm2 B. 0.81πm2 C. 2πm2 D. 3.24πm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某一工程,在工程招标时,接到甲、乙两个工程队的投标书.施工一天,需付甲工程队工程款1.2万元,乙工程队工程款0.5万元.工程领导小组根据甲、乙两队的投标书测算,有如下方案:①甲队单独完成这项工程刚好如期完成;②乙队单独完成这项工程要比规定日期多用6天;③若甲、乙两队合做3天,余下的工程由乙队单独做也正好如期完成.试问:
(1)两队单独做各要几天完成?
(2)在不耽误工期的前提下,你觉得哪一种施工方案最节省工程款?请说明理.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】补全下列各题解题过程.
如图,EF∥AD,∠1 = ∠2,∠BAC = 70°,求 ∠AGD 的度数.

解:∵EF∥AD ( 已知 )
∴∠2 = ( )
又∵∠1=∠2 ( )
∴∠1=∠3 ( )
∴AB∥ ( )
∴∠BAC + = 180°( )
∵∠BAC = 70°(已知 )
∴∠AGD = _ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班组织了一次读书活动,统计了16名同学在一周内的读书时间,他们一周内的读书时间累计如表,则这16名同学一周内累计读书时间的中位数是 .
一周内累计的读书时间(小时) | 5 | 8 | 10 | 14 |
人数(个) | 1 | 7 | 5 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC的顶点坐标为A(﹣2,3)B(﹣3,1)C(﹣1,2),以坐标原点O为旋转中心,顺时针旋转90°,得到△A′B′C′,点B′、C′分别是点B、C的对应点.
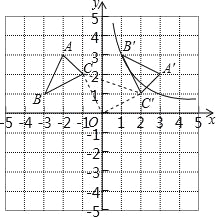
(1)求过点B′的反比例函数解析式;
(2)求线段CC′的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E、B、F、C四点在一条直线上,EB=CF ,∠A =∠D,添以下哪一个条件仍不能证明△ABC ≌△DEF的是( )

A. ∠DEF=∠ABC B. DF∥AC C. AB∥DE D. AB =DE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△OAB如图所示放置在平面直角坐标系中,直角边OA与x轴重合,∠OAB=90°,OA=4,AB=2,把Rt△OAB绕点O逆时针旋转90°,点B旋转到点C的位置,一条抛物线正好经过点O,C,A三点.
(1)求该抛物线的解析式;
(2)在x轴上方的抛物线上有一动点P,过点P作x轴的平行线交抛物线于点M,分别过点P,点M作x轴的垂线,交x轴于E,F两点,问:四边形PEFM的周长是否有最大值?如果有,请求出最值,并写出解答过程;如果没有,请说明理由.
(3)如果x轴上有一动点H,在抛物线上是否存在点N,使O(原点)、C、H、N四点构成以OC为一边的平行四边形?若存在,求出N点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】服装店老板用45 000元购进一批羽绒服,由于深受顾客喜爱,很快售完.老板又用49 500元购进相同数量的该款羽绒服,但每件进价比第一批多了9元.根据题中信息,解答下列问题:
(Ⅰ)第一批羽绒服每件进价是多少元?
(Ⅱ)老板以每件120元的价格销售该款式羽绒服,当第二批羽绒服售出![]() 时,出现了滞销,于是决定降价促销,若要使第二批的销售利润不低于14 000元,则剩余的羽绒服每件售价至少要多少元?(利润
时,出现了滞销,于是决定降价促销,若要使第二批的销售利润不低于14 000元,则剩余的羽绒服每件售价至少要多少元?(利润![]() 售价-进价)
售价-进价)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com