
 如图,∠ABC=50°,AD垂直平分线段BC于点D,∠ABC的平分线BE交AD于点E,连接EC,则∠AEC的度数是( )
如图,∠ABC=50°,AD垂直平分线段BC于点D,∠ABC的平分线BE交AD于点E,连接EC,则∠AEC的度数是( )| A. | 115° | B. | 75° | C. | 105° | D. | 50° |
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
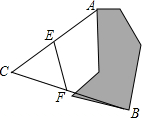 如图,现需测量池塘边上A、B两点间的距离,小强在池塘外选取一个点C,连接AC与BC并找到它们中点E、F,测得EF长为45米,则池塘的宽AB为90米.
如图,现需测量池塘边上A、B两点间的距离,小强在池塘外选取一个点C,连接AC与BC并找到它们中点E、F,测得EF长为45米,则池塘的宽AB为90米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
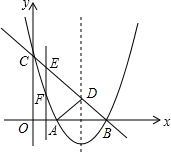 如图,某抛物线顶点坐标为(2,-1)与y轴交于点C(0,3),与x轴交于A、B两点
如图,某抛物线顶点坐标为(2,-1)与y轴交于点C(0,3),与x轴交于A、B两点查看答案和解析>>
科目:初中数学 来源: 题型:填空题
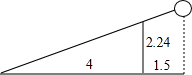 已知女排赛场球网的高度是2.24米,某排球运动员在一次扣球时,球恰好擦网而过,落在对方场地距离球网4米的位置上,此时该运动员距离球网1.5米,假设此次排球的运行路线是直线,则该运动员击球的高度是3.08米.
已知女排赛场球网的高度是2.24米,某排球运动员在一次扣球时,球恰好擦网而过,落在对方场地距离球网4米的位置上,此时该运动员距离球网1.5米,假设此次排球的运行路线是直线,则该运动员击球的高度是3.08米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k<2且k≠1 | B. | k>2且k≠1 | C. | k>2 | D. | k<2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com