
分析 (1)设A型店面x间,则根据“全部店面的建造面积不低于大棚总面积的80%”“不能超过大棚总面积的85%”列不等式求解即可得到40≤x≤55;
(2)根据“每年能有29.52万元的租金收入”作为相等关系列式解答即可.另外要考虑x的取值必须为整数;
(3)设月租费为W元,则W=400×75%x+360(80-x)×90%=-24X+25920,根据函数的单调性和自变量的取值范围可求得最值.
解答 解:(1)设A型店面x间,则:
2400×80%≤28x+20(80-x)≤2400×85%
解得:40≤x≤55;
(2)①令12×400×75%x+12×360(80-x)×90%=295200,
则x=$\frac{2005}{36}$,x不是整数
所以,目标不能实现.
②设月租费为W元,则
W=400×75%x+360(80-x)×90%=-24x+25920
由于W随着x的增大而减小,故当x=40时W最大,为24960元,
∴A、B两种类型的店面各建造40间时,店面的月租金最高,最高月租金收入是24960元.
点评 本题考查一元一次不等式组的应用,将现实生活中的事件与数学思想联系起来,读懂题列出不等式关系式即可求解.要会根据自变量的取值范围结合函数的单调性求函数的最值问题.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:选择题
| A. | a>-36 | B. | a≥-36 | C. | a<-36 | D. | a≤-36 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
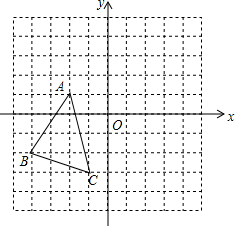 如图,在平面直角坐标系中,△ABC的顶点都在网格点上,将△ABC先向右平移5个单位长度,再向上平移2个单位长度,得到△A′B′C′.
如图,在平面直角坐标系中,△ABC的顶点都在网格点上,将△ABC先向右平移5个单位长度,再向上平移2个单位长度,得到△A′B′C′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | xy-1 | B. | $\frac{1}{{x}^{2}+1}$ | C. | x2+xy2 | D. | $\sqrt{{x}^{4}+1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,∠ABC=50°,AD垂直平分线段BC于点D,∠ABC的平分线BE交AD于点E,连接EC,则∠AEC的度数是( )
如图,∠ABC=50°,AD垂直平分线段BC于点D,∠ABC的平分线BE交AD于点E,连接EC,则∠AEC的度数是( )| A. | 115° | B. | 75° | C. | 105° | D. | 50° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com